广告
用于路径跟踪的几种不同形式的车辆运动学模型
在自动驾驶车辆路径跟踪控制系统设计中，经常使用车辆的运动学模型，这种模型完全基于车辆运动特性的几何关系建立，不考虑影响运动的力特性，使用时模型简单，便于分析。本文将介绍几种常用的车辆运动学模型。
1、以前轴中心为车辆中心的运动学模型
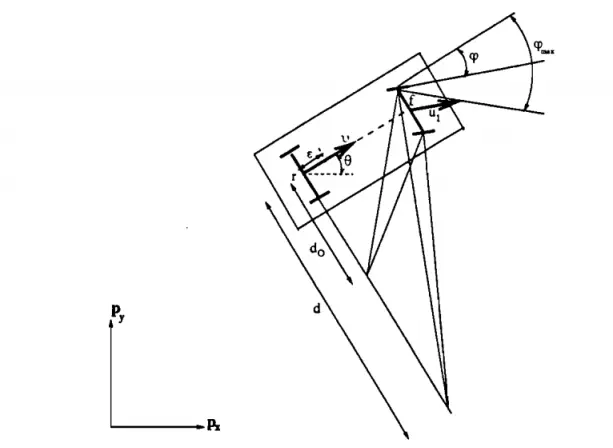
图1 车辆模型
其中，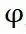
为前轮转向角，
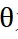为横摆角，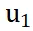
为车辆前轴速度，
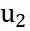为前轮转角速度，f为前轴中心，r为后轴中心，v为后轴的速度，e为轴上任意一点到后轴中心的距离。
由勾股定理可知：
其中，R为转弯半径，L为轴距。
刚体的角速度等于它的线速度除以线速度到速度瞬心的距离R，即：
把(4)带入(5)中可得：
以前轴中心为车辆中心的运动学模型如下所示：
2、以后轴中心为车辆中心的运动学模型
把前轴中心的坐标转化为后轴中心的坐标:
式(8)对t求导可得：
将式(1)、式(2)和式(6)带入上式可得：
以后轴中心为车辆中心(速度是前轴中心的速度)的运动学公式：
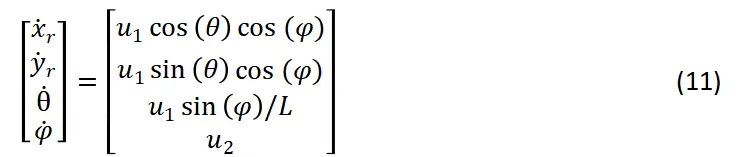
由速度投影公式可知：
将上式带入式(11)中可得以后轴中心为车辆中心的运动学公式：
3、以轴上任意一点为车辆中心的运动学模型
把后轴中心的坐标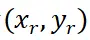
转化为轴上任意一点的坐标
：
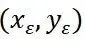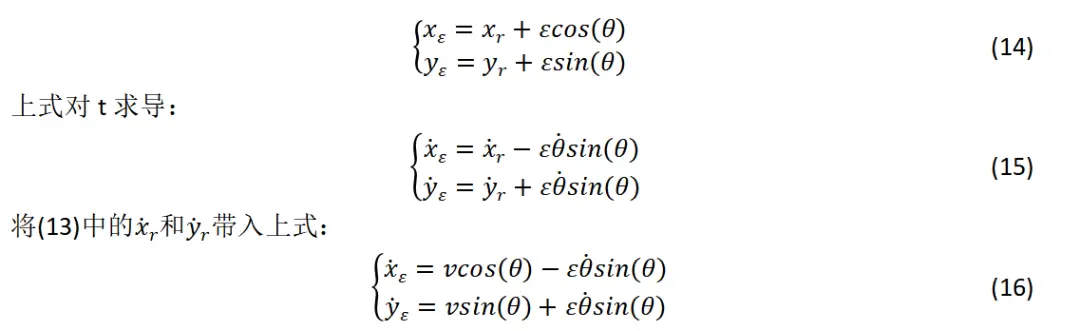
以轴上任意一点为车辆中心的运动学公式:
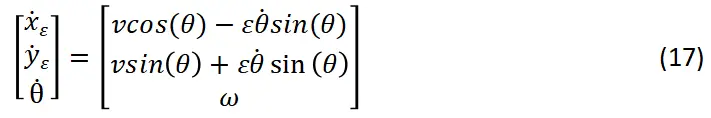
上式中的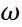
为横摆角速度。
4、考虑质心侧偏角、以质心为中心的运动学模型
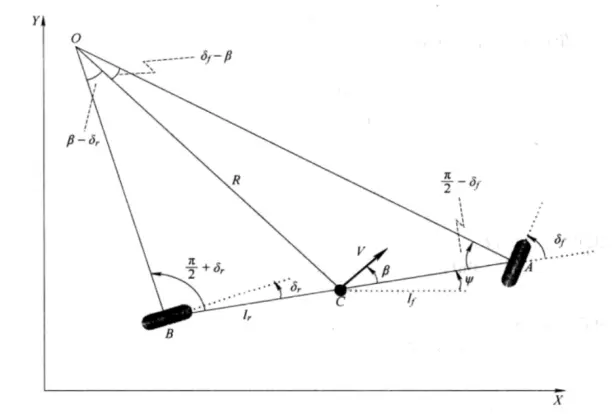
图2 自行车模型
其中，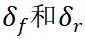
分别为前后轮转角，
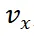为质心侧偏角，
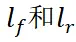分别为质心到前后轴的距离，R为转弯半径，C为质心，O为速度瞬心，A和B分别为前后轴中心。
由勾股定理可知：
一个刚体的角速度等于它的线速度除以线速度到速度瞬心的距离，即：
由正弦定理可知：
把公式(4)带入(3)中得：
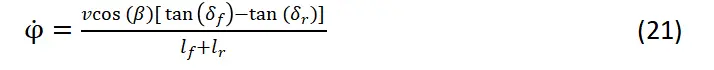
考虑质心侧偏角、以质心为中点的运动学公式:
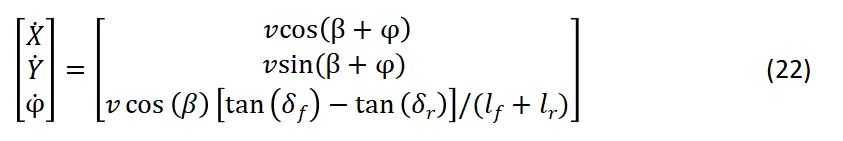
若后轮不转向:
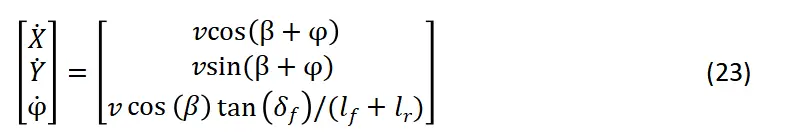
车辆低速时，可假设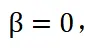
上式则将简化为如下形式，这也是常用的一种运动学模型
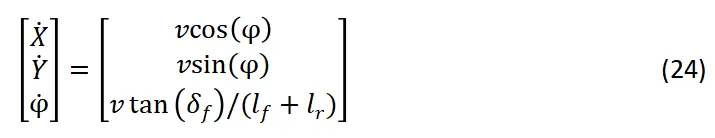
5、以后轴中点为车辆中心的第二种运动学模型
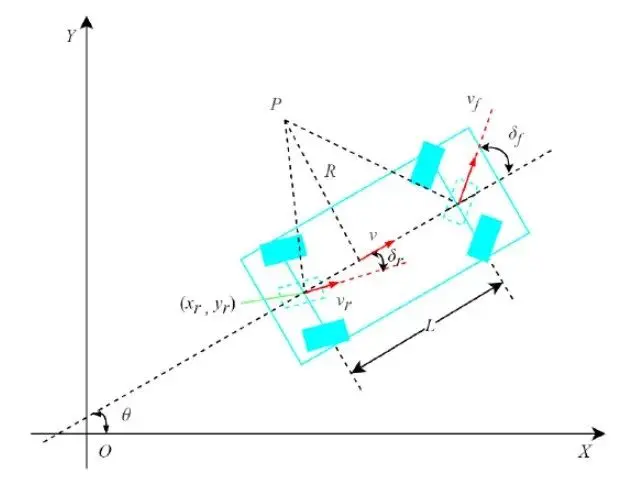
其中，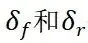
分别为前后轮转角且都为正值，正负号通过左正右负判断，
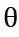为横摆角，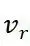
为后轴中心的速度，R为质心速度v对应的转弯半径，P点为速度v的瞬心，L为轴长。
对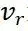
进行分解可得：
由速度投影定理可知：
与式(20)相同得到R：
通过式(26)和式(27)可得横摆角速度：
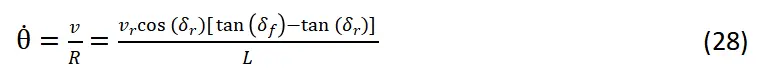
根据上述推导，最终得到车辆后轴中点位置的运动学方程如下：
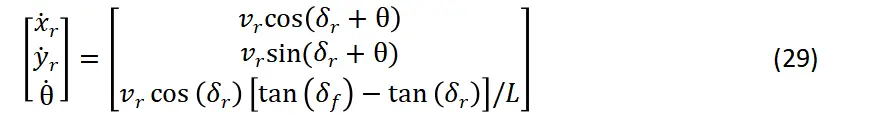
6、Frenet坐标系下的运动学模型
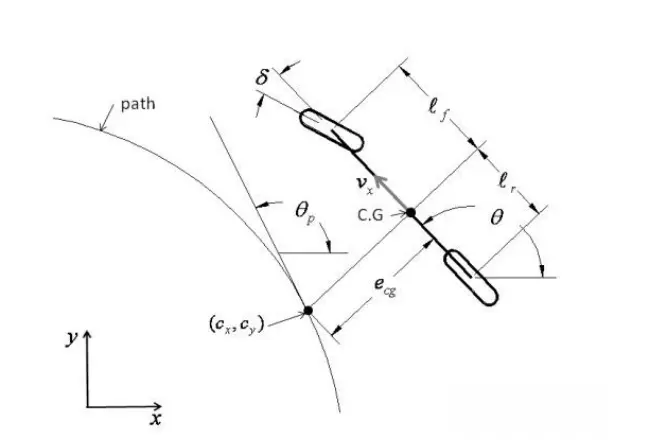
图4 道路坐标系下的车辆运动学模型
其中，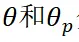
分别为横摆角和参考横摆角，
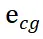为横向误差，
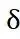为前轮转角，
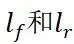分别为质心C.G到前后轴的距离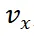，为质心的速度。
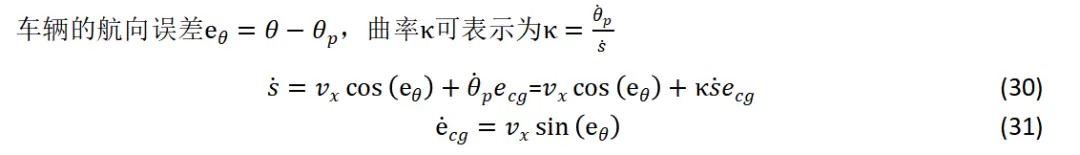
联立上式可得车辆在frenet坐标系下的运动学方程如下，这也是在自动驾驶中经常使用的一种运动学模型，尤其是在车道保持和GPS循迹行驶中。
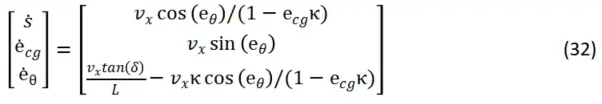
综上，本文介绍了6种不同的车辆运动学模型，其中使用最多的是模型（24）和（32），这两个模型分别应用于不同的坐标系。
广告 
广告
编辑推荐
最新资讯
-
测迅乌镇&盐城测试场：助力智能网联汽车标
2025-02-22 12:39
-
使用示波器对三相电机驱动器进行测量
2025-02-22 12:37
-
上汽集团大乘用车重磅招聘
2025-02-22 12:25
-
GB/T 44173-2024对开门预警DOW的要求
2025-02-22 12:25
-
声音工程：像用PS一样编辑声音
2025-02-21 17:04
广告
广告
