轮胎道路摩擦系数的基本估计：一种基于模型的学习框架

编者按：这篇文章提出了一种基于模型学习的交通流阻力系数（TRFC）识别方法，结合事件触发的容积卡尔曼滤波（ETCKF）和扩展卡尔曼神经网络（EKFNet），以提高车辆运动性能与安全性。针对测量噪声未知和数据丢失问题，ETCKF通过事件触发机制处理传感器数据缺失，并将处理后的数据输入非线性轮胎模型计算归一化轮胎力；EKFNet则利用轮胎受力信息和车辆模型实现TRFC估计。虚拟实验表明，该方法在加速、减速和转向等多种驾驶条件下优于传统卡尔曼滤波器，且适用于分布式驱动电动汽车和传统燃油车。但需注意的是，当前框架基于两轴车辆模型，对多轴挂车等特种车辆存在局限性，且因实验条件限制尚未进行实车验证，未来将进一步完善实车测试。

本文译自：

《Fundamental Estimation for Tire Road Friction Coefficient: A Model-based Learning framework》

文章来源：

IEEE TRANSACTIONS ON VEHICULAR TECHNOLOGY, VOL. 74, NO. 1, JANUARY 2025

作者：

Yan Wang 1 , Guodong Yin 2 , Peng Hang 3 , JingZhao 4 , Yilun Lin 5, Chao Huang 1

作者单位：

1香港理工大学，2东南大学，3同济大学，4澳门大学，5上海人工智能实验室城市计算实验室

原文链接：

https://ieeexplore.ieee.org/abstract/document/10700775

摘要：准确的胎路摩擦系数（TRFC）对提高车辆的运动性能和安全性至关重要。本文提出了一种基于模型的学习方法，结合事件触发的容积卡尔曼滤波（ETCKF）和扩展卡尔曼神经网络（EKFNet）来识别TRFC。首先，设计了一种事件触发机制来评估测量数据是否丢失，并将其与容积卡尔曼滤波融合，构建ETCKF来处理传感器数据。随后，将这些处理后的数据输入到非线性轮胎模型中，以计算归一化轮胎力。其次，利用EKF和四层神经网络组成EKFNet，利用轮胎受力信息和车辆模型对TRFC进行估计。多个虚拟实验结果表明，基于模型的学习框架的估计性能优于传统的扩展卡尔曼滤波器和无迹卡尔曼滤波器。此外，该方法不仅适用于分布式驱动电动汽车，也适用于传统燃油汽车。

关键词：事件触发容积卡尔曼滤波，扩展卡尔曼神经网络，轮胎路面摩擦系数

Ⅰ 引言

本文的其余部分组织如下。不断提高车辆的运动性能和增强车辆安全性是学术界和工业界持续追求的目标[1]、[2]、[3]。近年来，已提出了多种先进的决策与轨迹规划[4]、[5]、车辆底盘控制[6]、[7]、[8]以及车队控制[9]、[10]技术以提升车辆安全性。分布式驱动电动汽车（DDEV）在近年来成为了热门的研究课题。与传统电动汽车相比，它具有更多的控制自由度，这使得车辆稳定性控制系统更适用，降低了车辆不稳定的风险[11]。由于轮胎是车辆与地面的唯一连接部件，车辆的运动控制或稳定性控制最终都转化为对电机扭矩和制动扭矩的控制。轮胎与路面的摩擦系数（TRFC）直接限制了车辆可用的最大轮胎力。此外，许多高级驾驶辅助系统或高级别自动驾驶汽车需要根据 TRFC 动态调整纵向和横向控制以提高车辆安全性，例如路径跟踪[12]、主动避撞[13]和电子稳定控制系统[14]。然而，车载传感器无法直接测量 TRFC。因此，基于车载传感器信息估算 TRFC 是一种常见的解决方案。目前，TRFC 估算主要有两种广泛使用的方法：使用专用传感器的直接测量，即基于外部传感器的方法，以及基于车载传感器的估算，即模型法。

在基于车外传感器的方法中，近年来一种流行的方法是将智能轮胎与交互式建模相结合以获取轮胎与路面附着系数（TRFC）。在轮胎内部安装了各种类型的传感器，例如加速度计[15]、[16]、[17]、声学传感器[18]和压电传感器[19]等。此外，还有一些利用计算机视觉来估计TRFC 的方法已被提出[20]。Leng 等人[21]开发了一种视觉融合方法用于检测 TRFC，而 Yu 等人[22]则利用图像数据和反向传播神经网络来识别 TRFC。由于轮胎内部安装的传感器经常受到地面和其他障碍物（如岩石）的冲击，它们容易受损或脱落。基于视觉的方法通常严重依赖环境的可见度，并且此类方法只能获取 TRFC 的范围，而无法提供精确的数值。为此，基于模型的估计方法受到了越来越多的关注。

在直线行驶条件下，通过纵向动态模型实现对轮胎径向力系数（TRFC）的估计[23]。Rajamani 等人[24]设计了一种基于纵向滑移信息的 TRFC 估计方法。此外，Sharifzadeh 等人[25]利用递归最小二乘法，通过滑移信号来估计 TRFC。为了进一步提高估计精度，许多研究人员采用卡尔曼滤波器来估计 TRFC。此外，还有研究采用扩展卡尔曼滤波器（EKF）来识别 TRFC[26]。类似的 TRFC识别方法在[27]、[28]中也有记载。在转弯操作期间，Hu等人[29]基于车辆横向动力学设计了一种 EKF 来估计TRFC。

同样，后续的研究引入了基于扩展卡尔曼滤波（EKF）的估计器[30]。无迹卡尔曼滤波（UKF）的估计精度超过了EKF。因此，它被用于进一步提高 TRFC 的识别性能[29]、[31]、[32]。例如，Wang 等人[33]提出了一种基于 UKF 的集成估计方案，用于在质量不匹配的情况下预测 TRFC。此外，改进的 UKF 也被用于处理数据丢失情况下的 TRFC估计问题[34]。此外，容积卡尔曼滤波（CKF）也被用于TRFC 估计[35]、[36]。由于其跟踪能力有限，基于 DDEV模型的 TRFC 估计采用了增强版的强跟踪 CKF[37]。考虑到测量噪声可能呈非高斯分布，一些基于粒子滤波的方法被用于预测车辆状态[38]和 TRFC[39]、[40]。然而，由于计算成本高，粒子滤波在实际应用中面临挑战。

近来，随着深度学习算法能力的不断增强，无需考虑复杂的车辆或轮胎模型，数据驱动方法已被用于估计轮胎径向力系数（TRFC）。Mirmohammad 等人[41]收集了四个特征，并构建了一个多层神经网络来估计 TRFC。此外，还提出了一种时空卷积神经网络[42]来预测 TRFC。然而，过于复杂的网络结构可能会进一步增加计算成本。此外，这些数据驱动方法在可解释性方面往往具有挑战性，而且神经网络对车辆动力学的全面表征仍处于探索阶段。

通过上述分析，我们可以认识到基于模型的方法通常需要精确的噪声统计特性方面的先验知识才能实现最优估计结果。数据驱动的方法仍处于早期阶段，在数据收集和模型的泛化能力方面都存在挑战。此外，基于模型和数据驱动的方法都需要实时获取准确的传感器数据。为了解决上述挑战，提出了一种结合基于模型和数据驱动的估计方案，用于在测量噪声未知和数据丢失的情况下估计轮胎径向力系数（TRFC）。首先，设计了一种事件触发机制来评估测量数据是否丢失，并将其与容积卡尔曼滤波器（CKF）融合，构建事件触发容积卡尔曼滤波器（ETCKF）来处理传感器数据。随后，将这些处理后的数据输入非线性轮胎模型以计算归一化轮胎力。最后，由扩展卡尔曼滤波器（EKF）和四层神经网络组成的 EKFNet 利用轮胎力信息和车辆模型来估计 TRFC。主要贡献如下：

（1）与传统忽略数据丢失影响的 TRFC 识别方法不同，设计了一种 ETCKF 算法来处理车载传感器数据丢失的问题。

（2）与纯模型驱动或纯数据驱动的估计方法不同，提出了一种将模型驱动和数据驱动方法相结合的 EKFNet 来估计交通流状态。

（3）多个虚拟实验结果表明，所提出的估计方案能够准确识别TRFC 。

Ⅱ 系统建模

实现 TRFC 的实时识别需要开发精确的车辆和轮胎模型。考虑到计算成本、模型复杂度以及获取模型参数的难度，开发了一个四轮车辆模型来描述车辆的动态响应。此外，使用杜戈夫轮胎模型来计算轮胎力。

A.车辆模型

如图 1 所示，采用四轮车辆模型（FWVM）[43]。忽略空气阻力和悬架系统的影响。前轮具有相同的转向角，而后轮不具备转向能力。尽管假设前后轴的宽度相同，但为了不失一般性，我们仍用不同的变量来描述它们。此外，假定车辆重心与坐标系原点重合。FWVM 的相关方程如下。

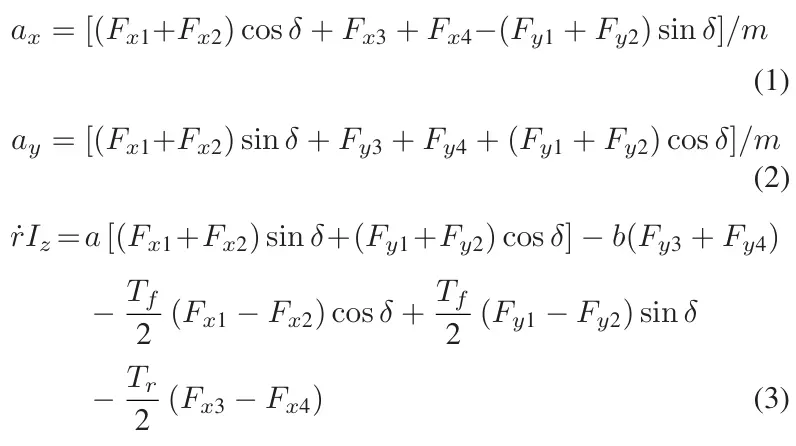
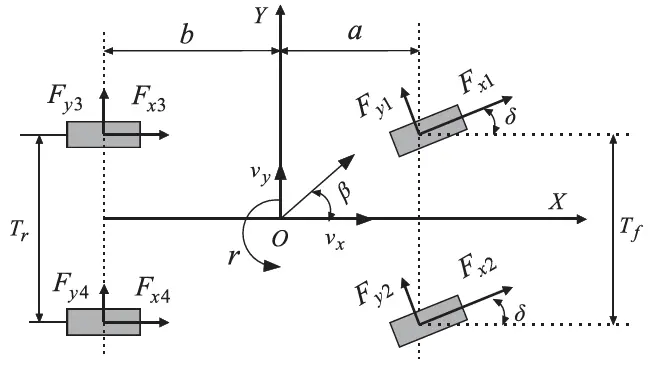
图1 四轮模型

其中，分别表示侧滑角、车辆纵向速度和车辆横速度，和分别代表车轮的前轮距和后轮距，表示车辆绕垂直轴的转动惯量，参数和分别表示车辆质心到前轴和后轴的距离，为车辆质量，为前轮转角，为车轮转速，分别对应左前轮、右前轮、左后轮和右后轮。和分别为纵向轮胎力和横向轮胎力，为车轮半径，为横摆角速度。

B.Dugoff轮胎模型

轮胎运动与力之间的相关性由 Dugoff[44]轮胎模型来描述。具体方程如下：

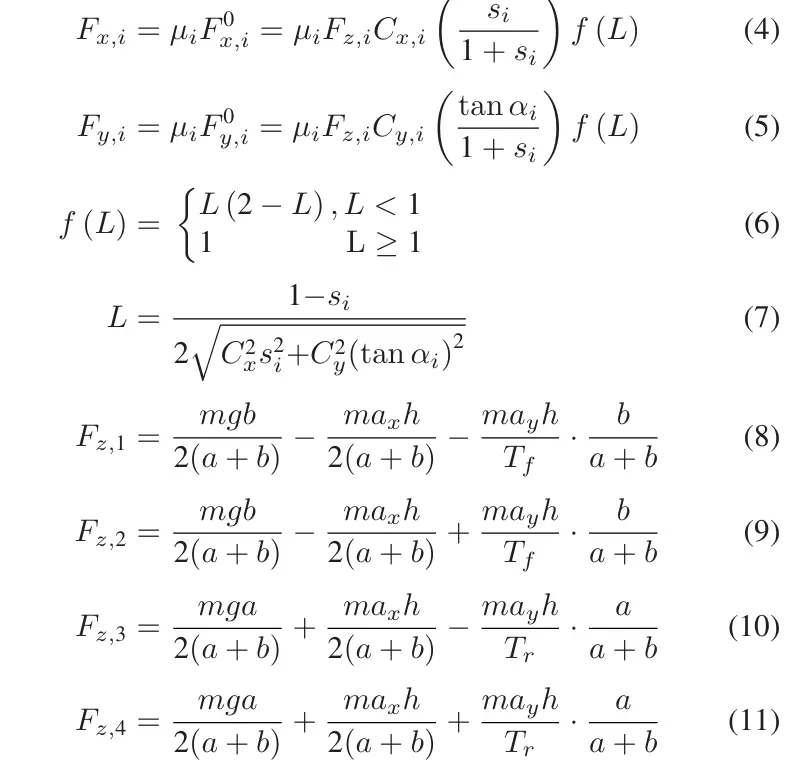
其中是胎路摩擦系数，是纵向和横向加速度，表示质心高度，分别表示纵向滑移率和质心侧偏角，分别表示轮胎的纵向和横向刚度系数以及垂直轮胎力，是归一化的纵向和横向力，，其具有与 FWVM 相同的物理意义。

Ⅲ 估计方案

A.估计框架

图 2 展示了整体的估计架构。对于在道路上行驶的车辆，我们可以基于诸如转向系统、制动系统等各子系统的总线信号获取带有测量噪声的信号。同时，由于电磁干扰等因素，这些信号并非总是完整的。因此，部分测量信号会受到噪声干扰和数据丢失的影响。由于这些信号通常具有不同的单位，所以首先会对数据进行归一化处理。随后，设计了一个事件触发规则来衡量数据丢失的程度。在发生数据丢失的情况下，仅采用CKF 的时间更新步骤进行数据处理。否则，将使用标准 CKF进行数据滤波。由 CKF 和事件触发规则融合而成的方法被称为 ETCKF。ETCKF 处理后的数据将输入到 Dugoff 轮胎模型中，以计算归一化的纵向和横向轮胎力。EKFNet 然后根据轮胎力信息和车辆模型实时估计 TRFC。

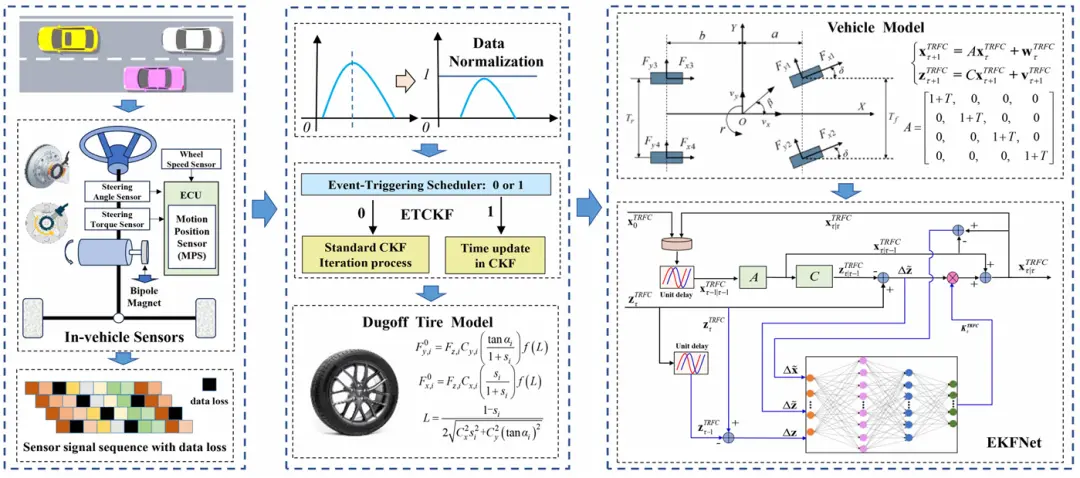
图2 基本估计方案

B.ETCKF

ETCKF 的总体方案如图 3 所示，显然，我们首先需要计算归一化的纵向力和横向力。方程（4）-（16）表明需要各种车载传感器信息，例如加速度、横摆角速度和其他类型的数据。此外，这些数据通常带有测量噪声，并且可能容易丢失数据。因此，直接将数据输入滤波器可能会导致滤波性能下降甚至发散。在此基础上，我们设计了一个切换规则：在数据丢失的情况下，我们仅使用滤波的时间更新方程；当没有数据丢失时，我们执行完整的滤波计算过程。在这里，我们选择 CKF 作为基础滤波器，因为 CKF 通过采用确定性采样方法能够更准确地捕捉非线性关系。

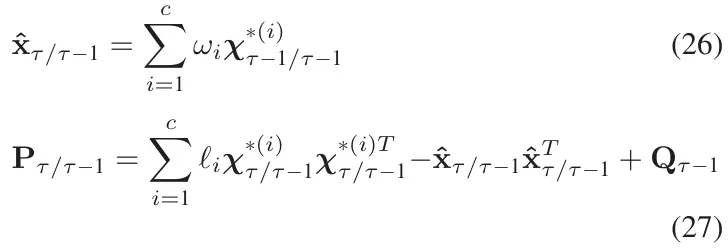
图3 ETCKF方案

（1）事件触发调度器

为了处理这些数据，我们首先建立如下状态空间模型。

其中，表示状态转移函数，为过程噪声，为测量噪声，为测量向量，表示测量转移函数，为输入向量，表示状态向量。

我们确立以下事件触发规则。

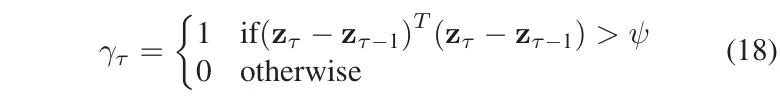
向向量中的信号添加了测量噪声。与具有相同的元素，是在时间时的归一化测量向量，表示在时间之前的归一化测量向量，是事件触发阈值。设为事件触发指示器。当时，表明出现了严重数据丢失的情况。在此期间，仅利用 CKF 的时间更新过程进行数据处理，排除测量更新过程以减轻数据丢失的影响。当时，则应用正常的 CKF 过滤来处理数据。

（1）CKF 的程序步骤如下：

1）初始化

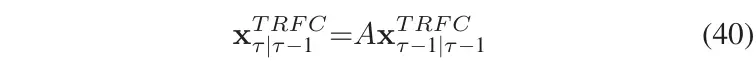
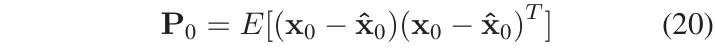
在（19）-（20）式中，表示数学期望，表示协方差矩阵。

的求积点（CP）及其对应的权重，记为，可通过以下步骤确定：

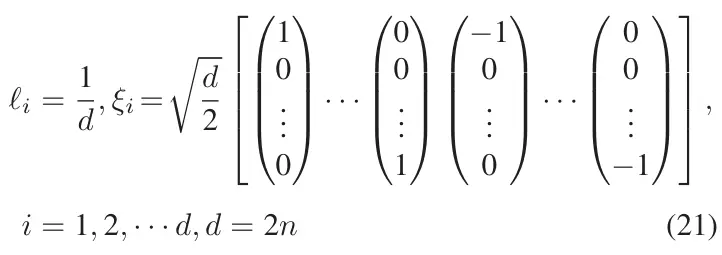
2）时间更新

矩阵的奇异值分解

其中表示为一个对角矩阵。随后，协方差矩阵，记作，可以表示为

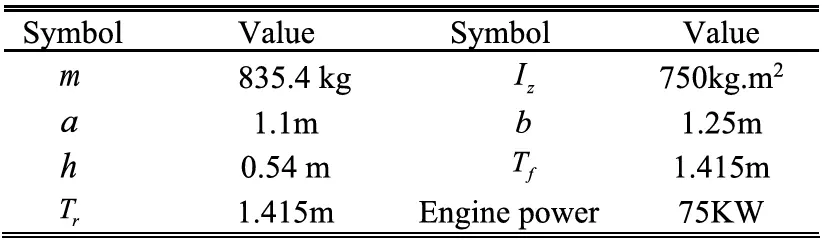
计算CP

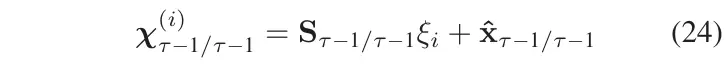
其中是状态预测值，是的CP。

更新已传播的CP

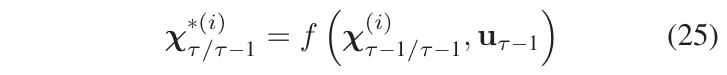
更新

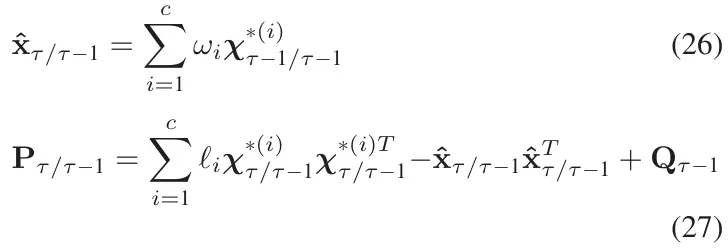
其中，表示的协方差矩阵。

3）测量更新

矩阵的奇异值分解

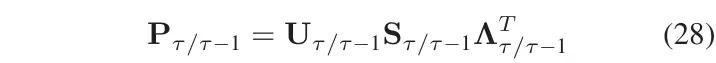
计算CP

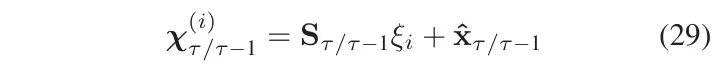
更新已传播的CP

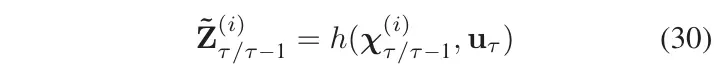
预测的测量向量、创新协方差矩阵，和交叉协方差矩阵分别由式给出

C.TRFC估计

图 4 展示了 TRFC 的总体框架。首先，来自 ETCKF 的传感器数据输入到Dugoff轮胎模型中进行计算，以获得归一化的纵向和横向轮胎力。基于这些轮胎力数据，使用 EKFNet 进行TRFC 估计。

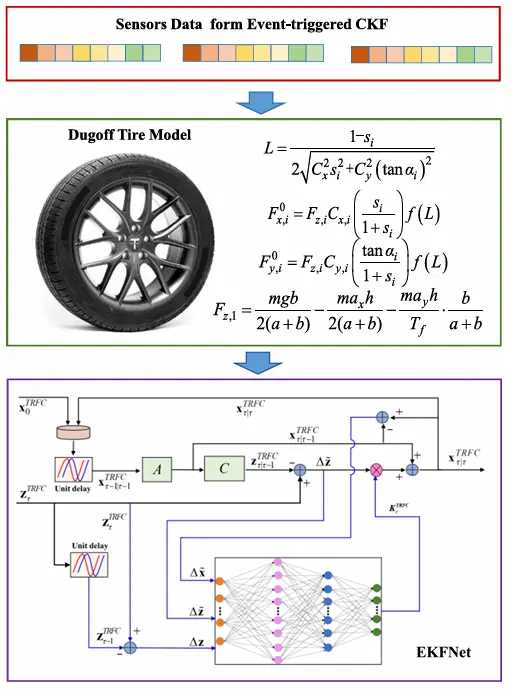
图4 TRFC方案

TRFC可以被认为在一个短时间间隔内是恒定的。 利用式(4)-式(5)中定义的与, 与之间的联系，可由式(1)-式(3)导出离散数学模型。

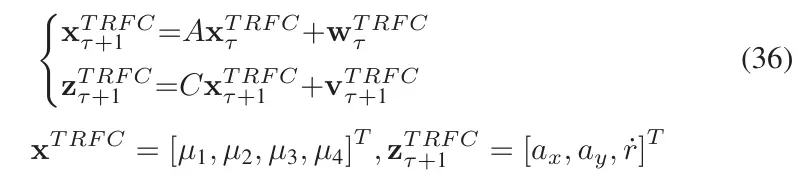
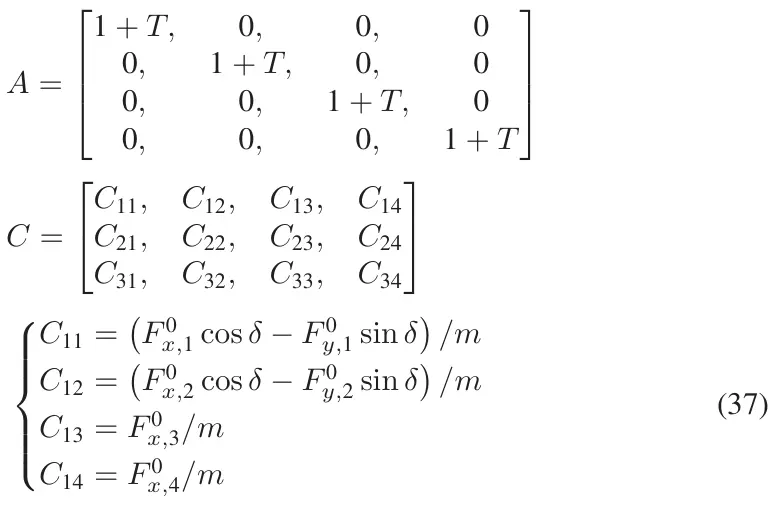
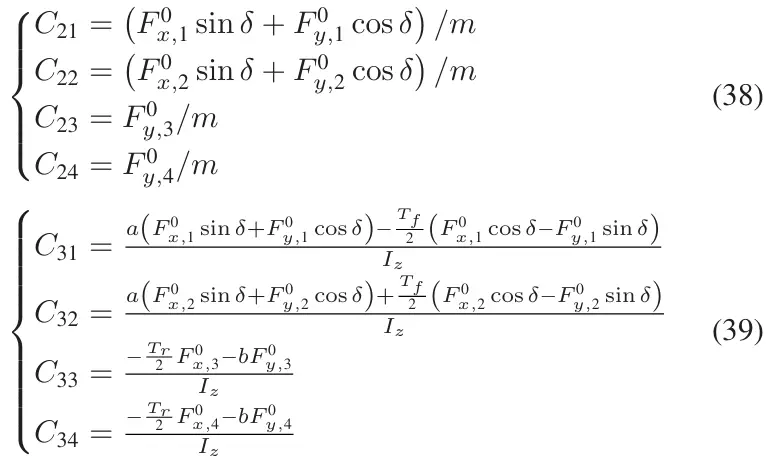
其中为采样时间间隔，其他变量含义与(1)-(3)相同。

接下来，利用EKFNet估算TRFC。 EKFNet是神经网络和传统EKF的结合。 利用神经网络直接预测卡尔曼增益，减轻了未知测量噪声的干扰。 虽然我们使用ETCKF来处理传感器信息，但传统的CKF依赖于对噪声统计特征的先验知识。 此外，由于老化等因素，机载传感器的噪声特性会发生动态变化。 此外，由于这些测量信号不是来自同一个传感器，因此测量噪声是多种多样的。 例如，滑移比的计算涉及到轮速，轮速是由轮速传感器获得的。 偏航率是由陀螺仪得出的。 因此，在执行TRFC估计时，通常要解决噪声不确定性问题。 TRFC估计的传统EKF迭代过程如下：

时间更新：

先前状态预测。

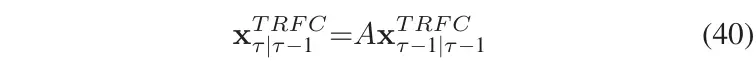
误差协方差预测。

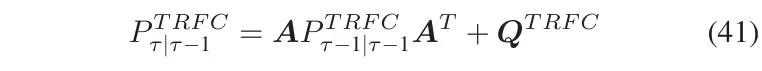
测量更新：

计算卡尔曼增益。

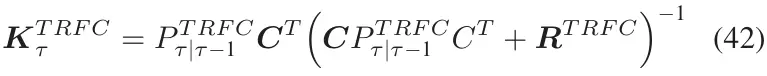
更新后验状态。

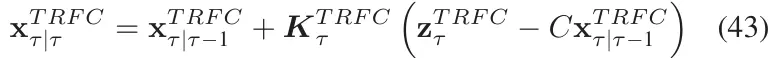
更新误差协方差。

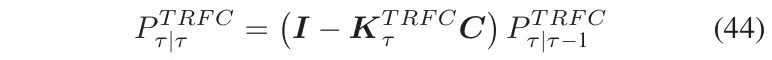
用流程图表示上述迭代过程，并将卡尔曼增益计算部分替换为神经网络预测模块。该框架如图 5 所示。

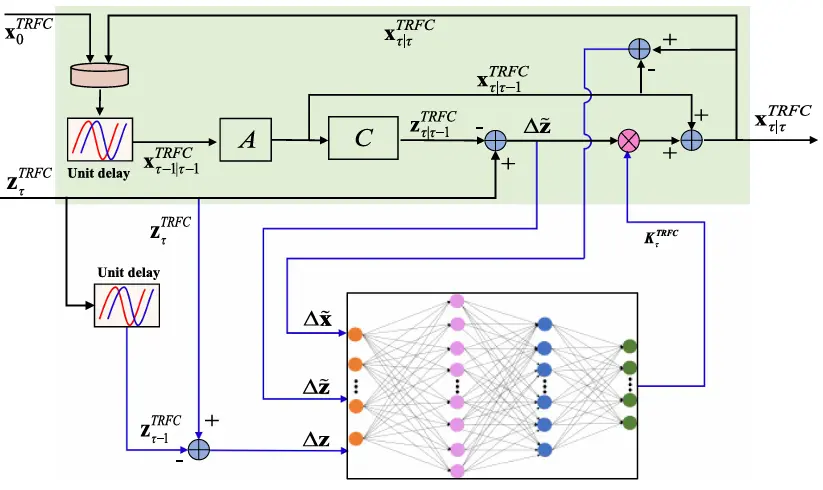
图5 EKFNet方案

EKFNet 是扩展卡尔曼滤波器（EKF）与四层神经网络的结合体。当测量噪声的统计特性未知时，它能够实现对交通流（TRFC）的精确估计。传统 EKF 中系统状态更新的关键在于卡尔曼增益的计算。从（42）式可以看出，R 对增益计算有直接影响。因此，从 EKF 中移除了负责计算卡尔曼增益的模块，转而利用四层神经网络模型直接预测卡尔曼增益。EKFNet 主要有两个模块：系统状态更新和卡尔曼增益预测。系统状态更新部分对应于图 5 中的浅绿色框，而卡尔曼增益预测部分主要是神经网络模型。

在系统状态更新模块中，首先利用前一时间步的状态值（记作）通过（40）式获得先验估计值。然后，利用和获得测量变量的预测值。最后，利用实际测量向量与预测测量向量之间的偏差以及卡尔曼增益和来得出精确的估计值。在卡尔曼增益预测部分，使用了一个四层神经网络来预测卡尔曼增益。众所周知，准确的增益计算取决于观测值和状态变量的统计特性。在为神经网络选择输入特征时，最好同时包含观测值和状态变量的信息。因此，通过计算这些变量在单位时间内的离散差分，可以有效地捕捉噪声的变化。最后，选择以下三个变量作为神经网络的输入。

(a) 前向更新误差：

(b) 观测误差：

(c) 创新误差：

可以看到四层神经网络接受输入。 然后，通过激活函数得到相应的滤波增益。 卡尔曼增益是4 ×3矩阵的12个元素，因为估计状态是四维的，有三个测量信号。 代价函数主要由神经网络的预测值与卡尔曼增益的真实值之间的偏差组成。 在训练过程中，我们使用反向传播算法对函数进行优化。 此外，我们使用梯度下降法来更新权重和偏差。 这种四层神经网络可以通过对大量数据的迭代训练直接预测卡尔曼增益。

此外，为了达到较高的预测精度，大量的训练数据是必不可少的。 我们开发了一个集CARSIM和SIMUlink于一体的仿真平台。 在SIMUlink中，部署了EKF算法，并且已知噪声的统计特性。 在这种情况下得到的卡尔曼增益数据可以作为训练场真值。 这辆车在不同的路面上以不同的速度行驶，如沥青、砾石、冰和雪。 在这些模拟中，引入了均值为零，方差范围为[0.0001,0.01]的白噪声。 在实验中，数据收集来自DDEV和传统燃油车（FV）。 我们总共积累了26000个样本。 然后策略性地划分数据：80%用于训练神经网络时，10%留给严格的测试，剩下的10%留给关键的验证。

Ⅳ 模拟试验

利用CARSIM和SIMUlink集成仿真平台验证了基于模型的学习估计方法的有效性。 高保真的车辆模型被整合到CARSIM软件中，提供更真实的动态响应。 因此，来自CARSIM的传感器信号和TRFC作为参考值（RV）。 车辆加速、减速和转向命令通过SIMUlink设置。 此外，ETCKF和EKFNet都在SIMUlink中执行。 我们在传感器信号中加入高斯噪声，然后将这些信号与阿伯努利分布相乘，生成具有数据dropout的传感器信号。 我们在高附着力路面（HARS）、中附着力路面（MARS）和对开路面（ORS）上进行验证试验，验证基于模型的学习方法的适用性。 值得注意的是，为了验证EKFNet的泛化，我们在DDEV和FV上都进行了实验。 重要的是，在最新版本的CARSIM软件中，电池和电机等模型已集成到软件中，在使用DDEV进行实验时不需要额外的建模工作。

A.ETCKF 的有效性

根据（17）式可知，我们有 11 个传感器信号，这些信号不可避免地会受到噪声和数据丢失的干扰。因此，我们设计了 ETCKF 来处理数据。在本研究中，通过软件在环实验多次调试，获得了事件触发的阈值，其值为 0.0013。ETCKF 中过程噪声和测量噪声的具体矩阵参数如下：

纵向加速度如图 6 所示。红色实线为原始数据（RV），绿色实线则表示添加了噪声且存在数据丢失情况下的信号。我们可以观察到，绿色实线在某些时段突然变为零，这表明出现了数据丢失的情况。紫色虚线表示 EKF 处理后的结果。蓝色虚线加点表示 ETCKF 的估计结果。

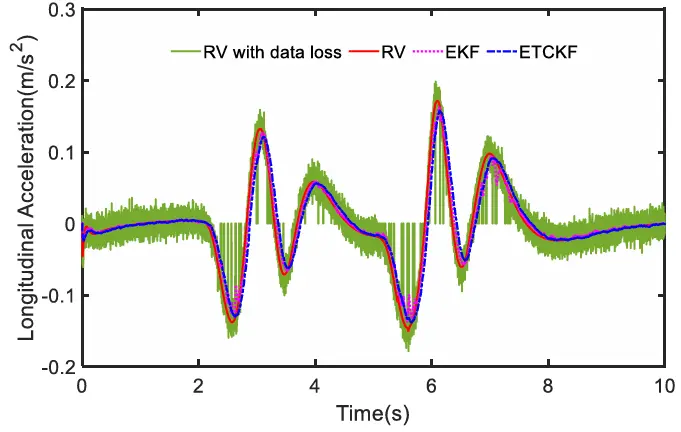
图6 纵向加速度

可以注意到，扩展卡尔曼滤波（EKF）的估计曲线在多个实例中出现了细微的波动，而扩展三角卡尔曼滤波（ETCKF）则更接近真实值（RV）。纵向速度、横向加速度和横向速度分别在图 7 至图 9 中给出。可以看出，与 EKF 相比，ETCKF 的曲线更平滑，也更接近真实值。

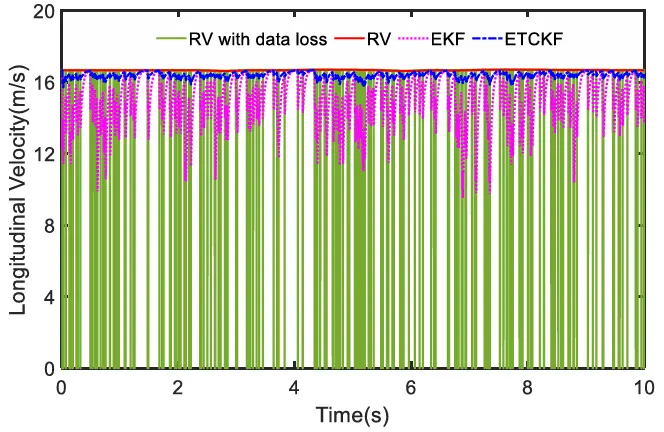
图7 纵向速度

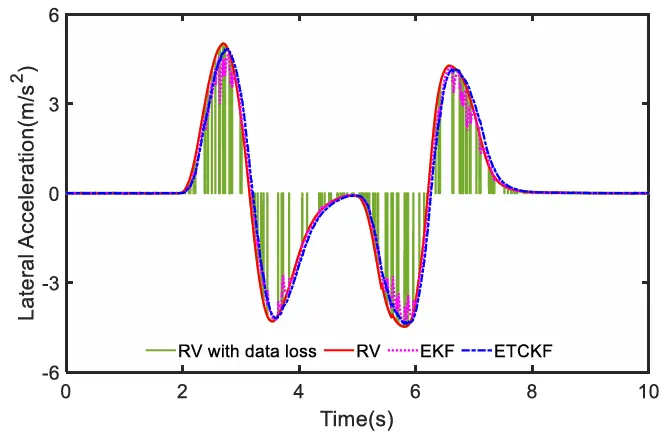
图8 侧向加速度

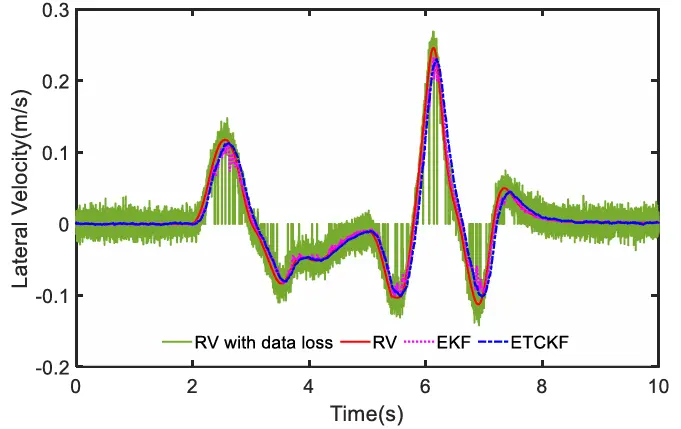
图9 侧向速度

前轮转向角如图 10 所示，在数据丢失的情况下，该曲线在某些时刻会突然变为零。横摆角速度曲线如图 11 所示，其变化趋势与前轮转向角的变化相关。为了更好地估计 TRFC，图 12 展示了横摆角加速度曲线，在此曲线中，ETCKF 继续表现出优越的性能。图 13 描述了车轮速度的变化，特别展示了左前轮的速度曲线。值得注意的是，由于四个车轮的速度曲线相似，因此仅展示了左前轮的速度曲线。这里以左前轮为例进行说明。可以观察到，在存在数据丢失的情况下，EKF 的车速波动曲线明显，而 ETCKF曲线波动较小，且与真实车速（RV）非常接近。

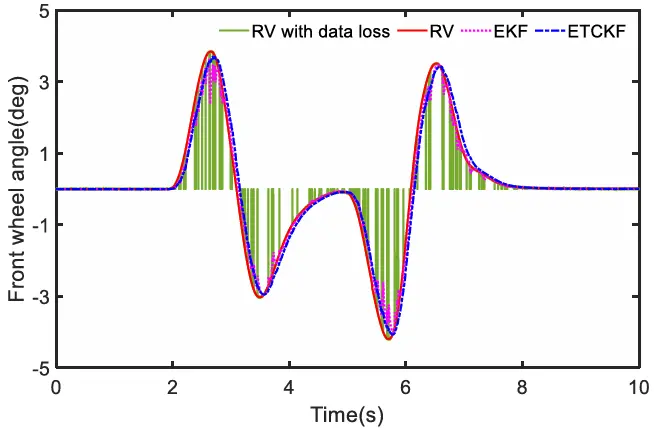
图10 前轮转向角

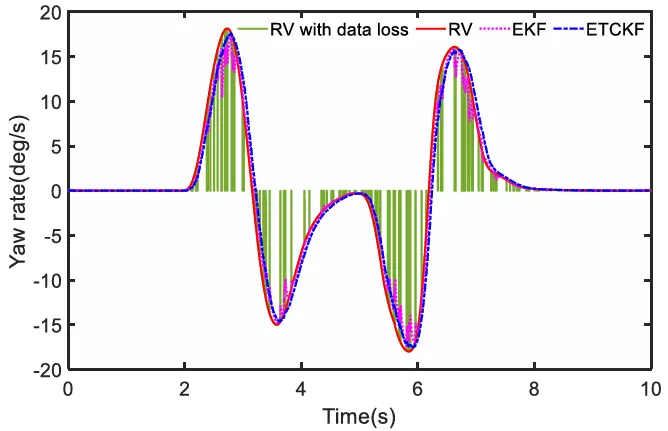
图11 横摆角速度

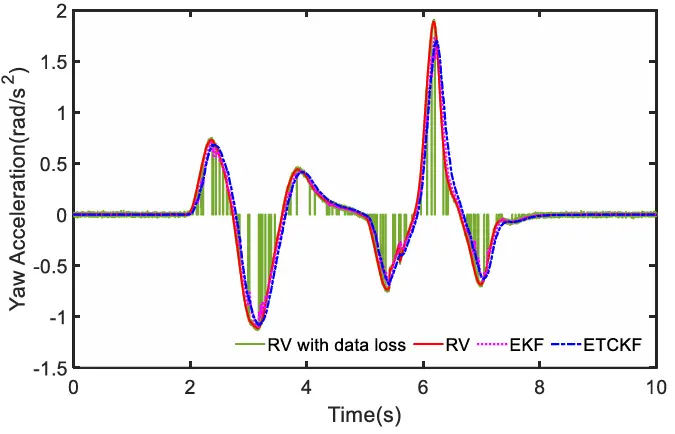
图12 横摆角加速度

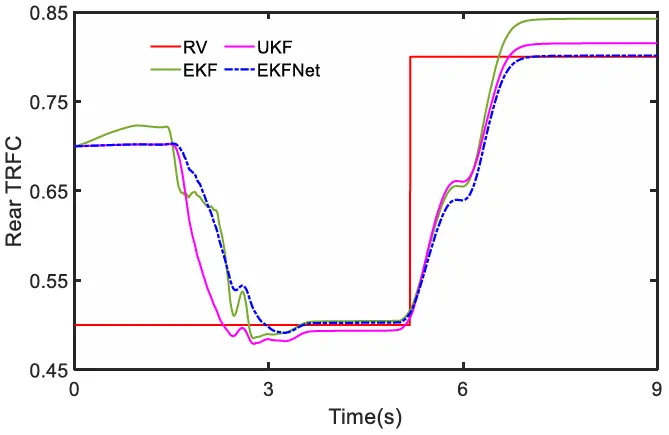
图13 左前车轮转速

B.利用 DDEV 进行 TRFC 估算

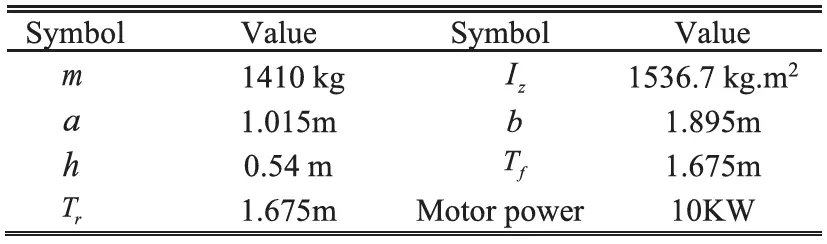
为了验证 EKFNet 的有效性，我们首先在 CARSIM软件中搭建了一个双车道测试场景。车辆由四个轮毂电机驱动，这些电机由相应的电池组供电，如图 14 所示。一些重要参数见表 I。

图14 双道变道测试

表I DDEV参数

（1）对向道路双车道变道测试：在对向道路上连续进行转向操作。在整个评估过程中，车辆将依次驶过高附着系数道路（HARS）和中等附着系数道路（MARS），其轮胎-道路附着系数（TRFC）值将从 0.85 变为 0.5。前轮角度如图 15 所示。在最初的 3.91 秒内，车辆行驶在高附着系数道路上，然后它移动到火星。车辆速度设定为固定的 60 千米/小时。为了验证 EKFNet 的有效性，我们将其与 EKF 和 UKF 进行了比较。不同算法的估计结果如图 16 和 17 所示。为了进行公平比较，测量噪声是随机生成的，EKF 和 UKF 中的 R 相同，并且偏离了真实值。这里，“前 TRFC”指的是左前轮和右前轮的平均估计结果。“后 TRFC”指的是左后轮和右后轮的平均估计结果。红色实线表示 TRFC 的真实值，品红色实线表示 UKF 的估计结果，绿色实线对应 EKF 的估计结果，蓝色虚线表示EKFNet 的估计结果。从图 16 可以看出，当转向开始时，所有三种算法都开始向真实值（RV）收敛。然而，EKFNet 的波动最小，并最终与 0.85 完全吻合。然而，随着 TRFC 从 0.8 变为 0.5，所有估计曲线都出现了超调，但 EKFNet 的波动最小。最终，EKFNet 的估计曲线迅速稳定在 0.5，而其他估计曲线则偏离了真实值。此外，UKF 的估计性能优于 EKF。这是因为 UKF 不需要求解雅可比矩阵，从而增强了其非线性逼近能力。EKFNet 利用神经网络直接预测卡尔曼增益，从而避免了雅可比矩阵计算所导致的精度降低。此外，大量的数据训练使得神经网络能够准确地预测卡尔曼增益。在多种噪声环境下，上述优势使得 EKFNet 的估计性能优于UKF。从图 17 可以看出，TRFC 的突变时间相较于图 16 有所滞后，这是因为前轮会先于后轮接触前方路面。在不同方法中，EKFNet 的估计精度最高。

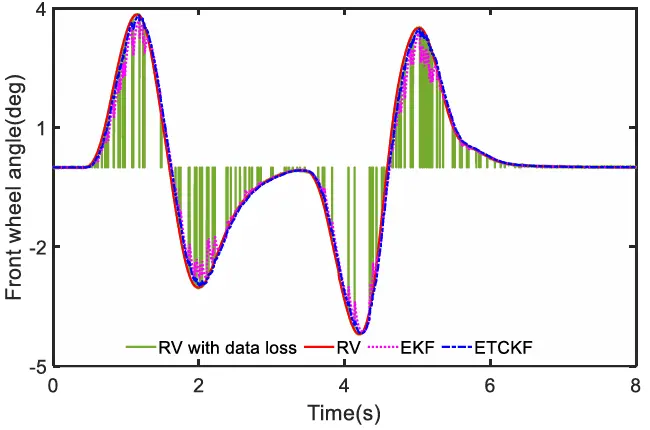
图15 ORS 上的前轮角度

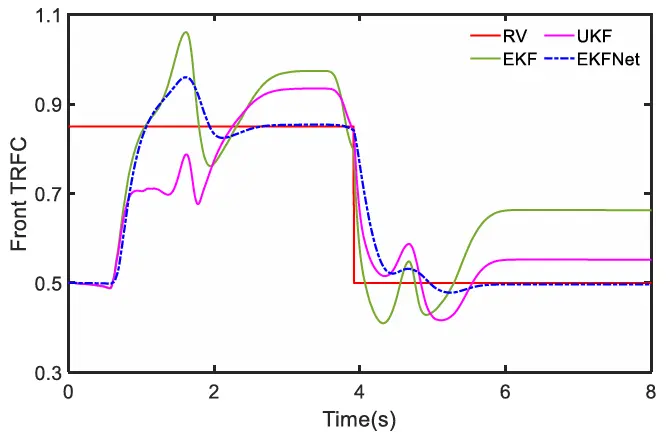
图16 ORS 上的前部 TRFC

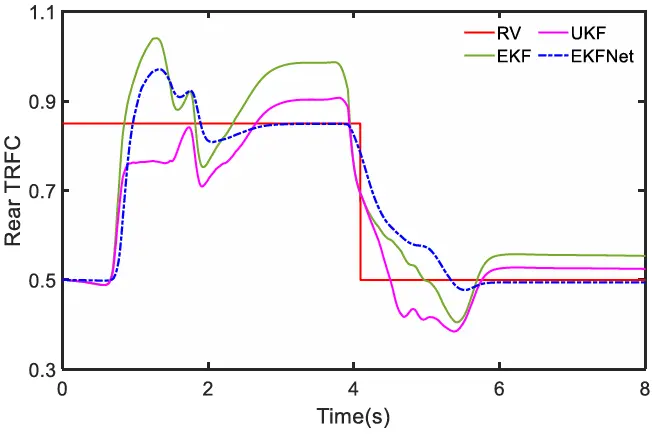
图17 ORS 上的后部 TRFC

（2）高附着系数路面的加速工况：在测试中，TRFC 设定为0.7，初始速度为 20 千米/小时，并进行加速操作。如图 18 所示，车辆速度持续上升。很明显，在数据丢失的情况下，EKF 曲线中的车辆速度波动明显更大，而 ETCKF 曲线的波动较小，并且与真实值（RV）的吻合度更高。不同估计算法的结果分别如图 19 和图 20 所示。在图 19 和图 20 中，由于加速操作在模拟开始时即已启动，因此可以观察到所有三种算法从一开始就能迅速收敛到真实值。这三种算法的收敛速度相似，但可以注意到，由于向扩展卡尔曼滤波器（EKF）和无迹卡尔曼滤波器（UKF）输入了不精确的噪声统计信息，这两个滤波器的估计曲线在 2 秒后与真实值的吻合度不佳。相比之下，EKFNet 一直保持着最佳的估计性能。

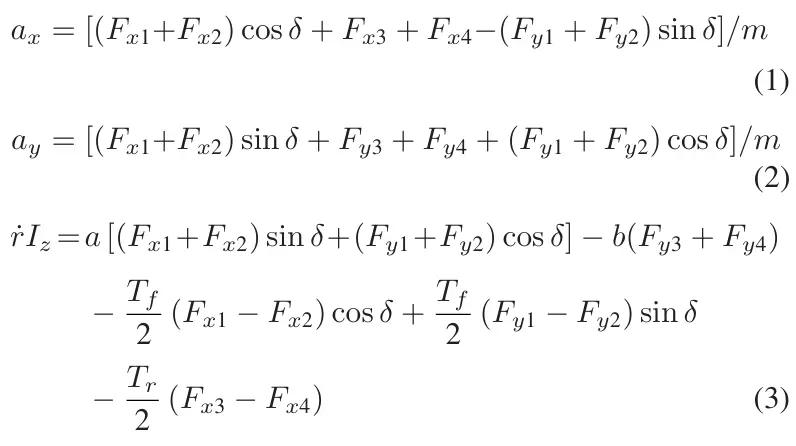
图18  HARS 上的纵向速度

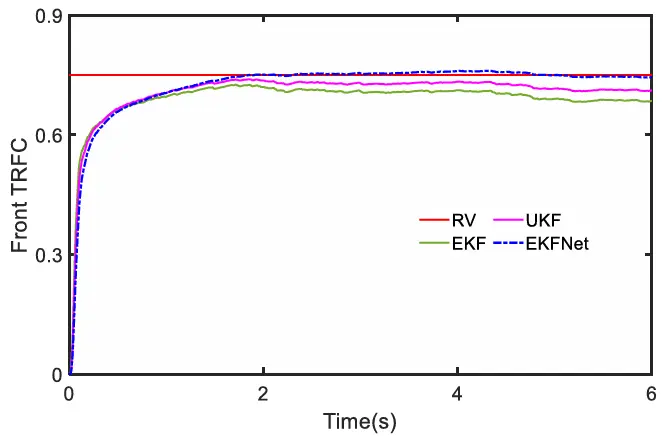
图19  HARS 上的前部 TRFC

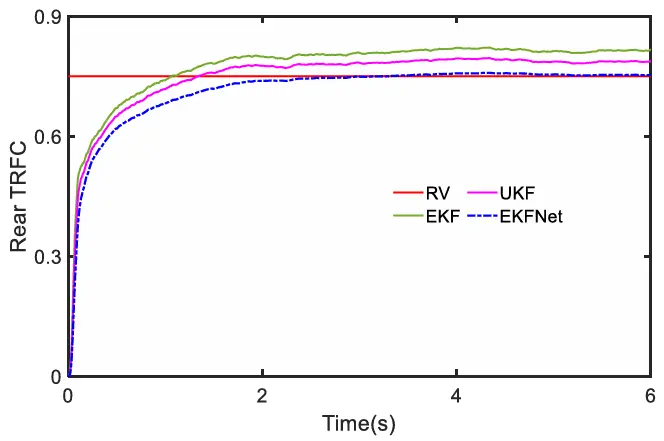
图20  HARS 上的后部 TRFC

（3）低附着系数路面的减速操作：我们在低附着系数路面（LARS）上进行了验证测试。测试中，TRFC 设置为 0.2，初始速度为 60 千米/小时，进行减速操作。如图 21 所示，车辆速度平稳下降。经过 ETCKF 处理后，速度曲线更平滑，更接近参考速度（RV）。各种估计算法的结果分别见图 22和图 23。在图 22 和图 23 中，由于一开始有显著的制动输入，这三种算法立即收敛到推荐速度（RV）。在模拟开始时，可以观察到三种算法在下降开始时都出现了超调现象，其中扩展卡尔曼滤波器（EKF）的超调幅度最大，而 EKFNet 的超调幅度最小。随后，三种算法都开始向真实值（RV）收敛。1 秒后，扩展卡尔曼滤波器（EKF）和无迹卡尔曼滤波器（UKF）的估计值出现了不同程度的偏差，而EKFNet 的估计曲线始终与真实值（RV）保持一致。

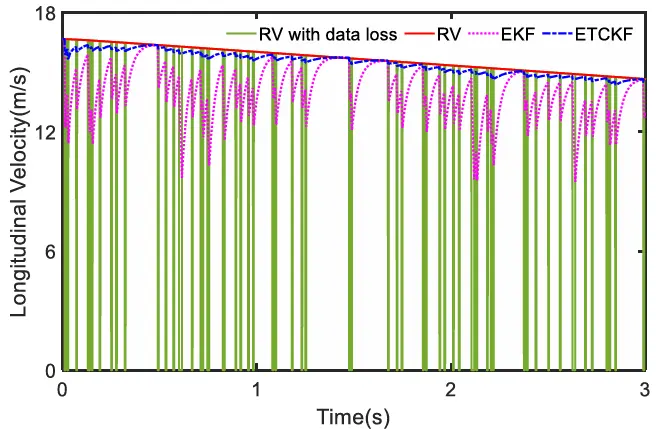
图21  LARS 上的纵向速度

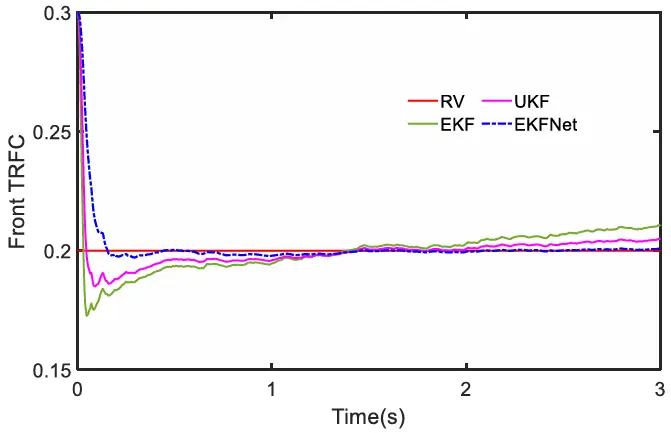
图22  LARS 上的前部TRFC

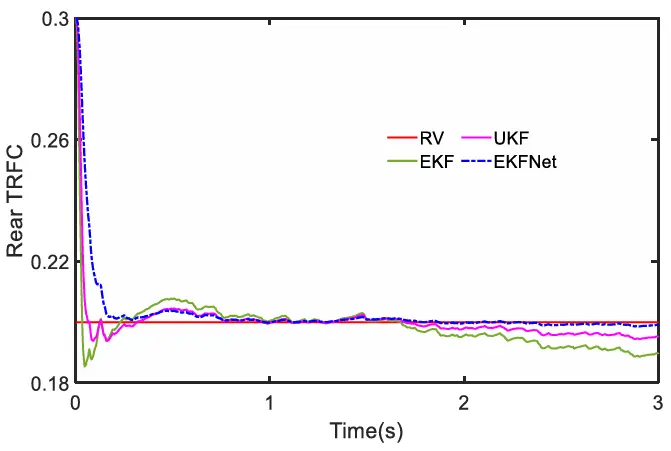
图23  LARS 上的后部TRFC

C.利用 FV 进行 TRFC 估算

为了进一步验证该算法的泛化能力，我们在图 24 所示的FV 数据集上进行测试。部分参数见表 II。在测试中连续执行转向操作。TRFC 从 0.5 变化到 0.8。

前轮转角如图 25 所示。经过 ETCKF 处理后，前轮转角曲线更平滑，更接近参考值。在最初的 5 秒内，车辆处于 MARS模式，随后切换到 HARS 模式。车辆速度固定为 54 千米/小时。各种算法的估计结果在图 26 和图 27 中给出。测量噪声是随机生成的。在扩展卡尔曼滤波（EKF）和无迹卡尔曼滤波（UKF）中，噪声协方差相同，且与真实值存在偏差。从图 26 可以看出，当转向开始时三种算法都开始向真实值收敛。值得注意的是，EKFNet 的波动最小，最终与真实值 0.5 完全一致。在从 0.5 到 0.8 的过渡期间，EKFNet 的估计曲线迅速稳定在 0.8，而其他估计算法则偏离了真实值。在图 27 中，类似的结果也很明显，EKFNet 展示出了最高的估计精度。

图24  使用 FV 进行的测试

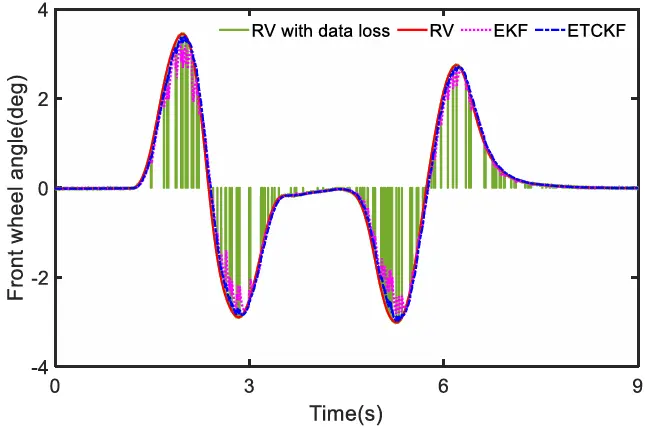
图25  FV 的前轮角度

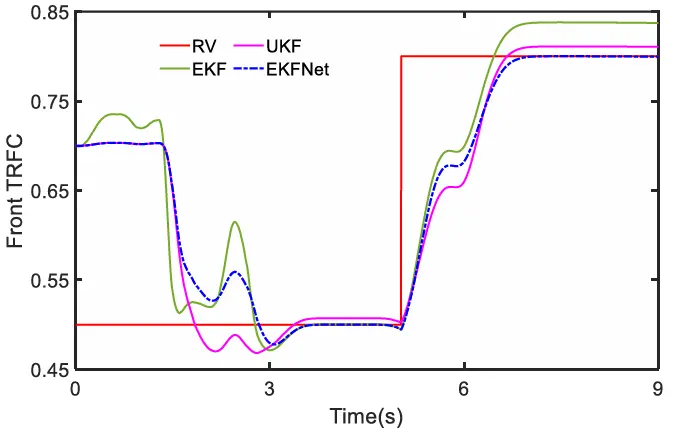
图26  使用 FV 进行的前部 TRFC 估计

图27  使用 FV 进行的后部 TRFC 估计

表 II  FV参数

从仿真结果可以看出，通过将所提出的算法部署到动态驾驶环境车辆（DDEV）或固定车辆（FV）中，可以实现对瞬态响应频率特性（TRFC）的精确估计。这是因为我们在车辆建模中使用了广义模型，从而削弱了动力传动系统模型的影响。其次，我们从 DDEV 和 FV 中收集数据，这增强了扩展卡尔曼滤波神经网络（EKFNet）的适用性。这些模型和算法的优势使得所提出的估计框架具有很高的通用性。

Ⅴ 结论

在本文中，针对测量噪声未知和数据丢失的情况，提出了一种基于模型的学习估计方案用于识别交通流阻力系数（TRFC）。首先，引入了扩展时间卷积卡尔曼滤波器（ETCKF）来解决测量信号缺失的问题。随后，设计了EKFNet 算法来估计 TRFC。通过电动汽车和燃油汽车的虚拟测试验证了所提出的方法能够在包括加速、减速和转向操作在内的各种驾驶条件下有效地识别 TRFC。

此外，需要指出的是，我们的估算框架基于两轴车辆模型，因此适用于普通乘用车。然而，对于多轴挂车等一些特种车辆，直接将所提出的方法应用于多轴挂车进行交通流量估算存在挑战。另外，由于缺乏实验场地和设备不齐全，当前算法尚未进行实车实验。一旦相关条件具备，将进行实车验证。

参考文献

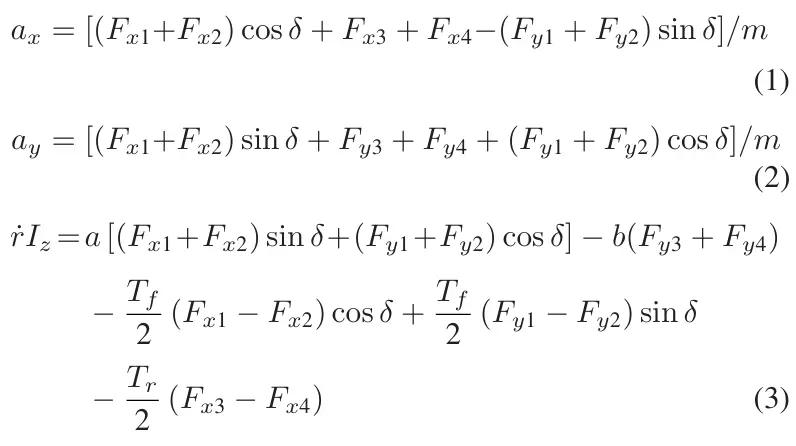
责编丨高炳钊