EVORA：面向风险感知越野自主系统的深度证据可通行性学习

编者按：随着无人系统在复杂野外环境中的应用日益广泛，地形可通行性评估成为提升自主导航能力的关键环节。本文由麻省理工学院与美国陆军研究实验室联合团队撰写，聚焦于风险感知越野导航中的不确定性建模问题，提出了一种基于深度证据学习的端到端方法——EVORA。该方法联合建模 Aleatoric 与 Epistemic 不确定性，通过Dirichlet分布与标准化流的结合，实现对牵引力分布的精确建模与未知地形的鲁棒识别，为部署于未知或高风险区域的自主机器人提供了坚实的数据驱动支撑。论文提出的 UEMD² 损失函数在保持准确率的同时，有效提升了对分布外地形的检测能力，具有较高的理论价值与应用潜力，值得从事智能驾驶、野外探测、风险规避导航等方向的科研人员深入研读。

本文译自：

《EVORA: Deep Evidential Traversability Learning for Risk-Aware Off-Road Autonomy》

文章来源：

IEEE Transactions on Robotics, vol. 40, pp. 3756-3777, 2024.

作者：

蔡小毅¹，Siddharth Ancha¹，Lakshay Sharma¹，Philip R. Osteen¹，Bernadette Bucher²，Stephen Phillips²，王久光²，Michael Everett¹，Nicholas Roy¹，Jonathan P. How¹

作者单位：

¹ 麻省理工学院（Massachusetts Institute of Technology）,² 美国陆军研究实验室（U.S. Army Research Laboratory）

原文链接：

https://ieeexplore.ieee.org/document/10606099

摘要：穿越具有良好牵引力的地形对于实现快速越野导航至关重要。现有方法并非基于地形特征手动设计成本，而是通过自监督直接从数据中学习地形属性，从而自动惩罚穿越不良地形的轨迹。然而，如何正确量化和降低学习模型中不确定性带来的风险仍存在挑战。为此，我们提出了证据越野自主性 (EVORA)，这是一个统一的框架，用于学习不确定性感知的牵引力模型并规划风险感知的轨迹。对于不确定性量化，我们通过学习离散牵引力分布和牵引力预测器潜在特征的概率密度，有效地对偶然不确定性和认知不确定性进行建模。利用证据深度学习，我们用网络输出参数化狄利克雷分布，并提出一种新颖的不确定性感知平方土方距离损失函数，该函数具有闭式表达式，可提高学习精度和导航性能。对于风险感知导航，所提出的规划器会模拟具有最坏情况预期牵引力的状态轨迹，以处理随机不确定性，并惩罚穿越具有高认知不确定性地形的轨迹。我们的方法已在模拟环境以及轮式和四足机器人上得到广泛验证，与假设无滑移、假设预期牵引力或针对最坏情况预期成本进行优化的方法相比，其导航性能有所提升。

关键词：自主机器人，自监督学习，不确定性量化，越野导航

Ⅰ 引言

本文的其余部分组织如下。

自主机器人正日益部署于矿区、森林、沙漠等恶劣的非铺装环境中，这些环境既需要对几何结构进行理解，也需要对语义信息进行解析，以便识别非几何危险（例如淤泥坑、光滑表面）和几何“非危险”区域（例如高草和灌木），从而实现可靠的导航。为此，近期的方法通常基于地形的语义分类手动分配导航代价，这一过程不仅需要大量专家知识来标注数据，还需训练出足够精确且语义类别丰富的分类器，以获得期望的风险感知行为。另一种思路是利用自监督学习直接从导航数据中学习可行性模型，以便在路径规划时自动对不利地形分配更高的代价。然而，由于真实环境下自监督的数据采集既缓慢又昂贵，仅仅增加数据量并不足以提升性能，除非我们能够对所学模型中的不确定性进行量化并据此进行风险缓解。在越野导航情境中，不确定性主要以两种形式出现，如图 1 所示。

图 1. EVORA 在学习地形牵引模型时，同时捕捉两类不确定性，其中牵引力定义为实际速度与指令速度之比。(a) 内禀不确定性（Aleatoric uncertainty）是由于观测不完全而产生的固有且不可消除的不确定性。例如，外观相似的地形由于机器人与植被之间的复杂相互作用，可能具有不同的牵引力值。(b) 模型不确定性（Epistemic uncertainty）是由于训练环境与测试环境分布转移带来的模型不确定性，这会在测试时限制学习模型的可靠性。

内禀不确定性（Aleatoric uncertainty）是指因观测不完整而产生的固有且不可消除的不确定性。例如，两块外观相同的地形对车载传感器而言可能无法区分，但却会导致车辆表现出截然不同的行为——此类不确定性通过增加数据量也无法降低。模型不确定性（Epistemic uncertainty）则源自测试时遇到的超出分布（OOD）输入，这些输入在训练数据中缺乏代表性。由于在危险环境中（如碰撞或悬崖边缘坠落）采集 OOD 数据往往不切实际，训练数据集与机器人在实际场景中所遭遇环境之间可能存在巨大差距。目前，越野导航领域的大部分研究要么专注于通过学习系统参数的分布而非点估计来处理内禀不确定性 [10], [11]，要么专注于识别 OOD 地形以应对模型不确定性 [12], [13], [14], [15]，但很少有工作同时量化这两类不确定性并在规划阶段缓解由此带来的风险。

为了实现快速且可靠的越野导航，本文同时关注上游的不确定性感知可行性学习问题和下游的风险感知导航问题。鉴于二者相互依赖，我们提出了EVORA（Evidential Off-Road Autonomy）管线，将前述的不确定性感知可行性模型与风险感知规划器紧密结合（见图 2）。为了规划快速轨迹，我们使用地形牵引力来刻画可行性，其中牵引力定义为实际速度与指令速度之比（例如，导致车轮打滑并降低速度的湿滑地面对应低牵引力）。此外，我们通过学习经验牵引力分布（捕捉内禀不确定性）和牵引力预测器潜在特征的概率密度（捕捉模型不确定性），高效地量化了两类不确定性。鉴于真实牵引力分布可能呈多模态（如图 1(a)所示，外观相似的植被可能对应不同牵引值），我们对离散化的牵引值学习类别分布以刻画多模态性。借助文献 [16] 提出的证据深度学习方法，我们将神经网络输出参数化为Dirichlet分布（类别分布的共轭先验），并提出了一种基于平方Earth Mover’s Distance（EMD）的新型不确定性感知损失。该损失具有闭式解，可高效计算，并较传统的基于交叉熵的损失更准确地捕捉离散牵引值之间的关系。为应对内禀不确定性，我们设计了一个风险感知规划器，该规划器在前向仿真时使用最坏情形下的期望牵引力，实验证明其性能优于或匹配于其他方法：包括基于名义牵引力的方法 [11]、基于期望牵引力的方法 [21]，以及直接优化最坏情形期望代价的方法 [22] 。为降低模型不确定性带来的风险，本文在牵引预测器潜在特征的概率密度上设定置信度阈值，以识别超出训练分布（OOD）的地形，并通过辅助规划代价主动避开这些风险区域。该方法在仿真环境以及轮式和四足机器人硬件平台上均进行了详尽验证，结果表明其具有可行性并显著提升了导航性能。

图 2. 所提出的考虑不确定性的可行性学习与风险感知导航方法概览。 (a) 数据采集阶段：我们驱动机器人通过感兴趣的地形，记录牵引力值、机器人位姿，并构建语义高程地图。随后，离线生成训练数据集——提取地形的语义与高程特征，并沿机器人所过路径估计经验牵引力分布。 (b) 不确定性建模：利用证据深度学习（Evidential Deep Learning）[16]，对离散化后的牵引力值学习类别分布，以刻画固有不确定性（Aleatoric Uncertainty）；同时，通过归一化流网络（Normalizing Flow Network）[17]对牵引力预测器潜在特征的密度进行建模，以估计认知不确定性（Epistemic Uncertainty）。整个网络采用以网络输出参数化的狄利克雷分布所定义的考虑不确定性的损失函数进行训练。 (c) 风险感知导航：对于固有不确定性，我们提出了一种基于牵引力分布左尾条件在险价值（Left-Tail CVaR）的风险感知规划器，结合基于采样的模型预测控制（MPC）方法[18]对机器人状态进行前向模拟；对于认知不确定性，则通过对牵引力预测器潜在特征密度设定阈值，识别并在辅助规划代价中惩罚，以规避预测不可靠的OOD（分布外）地形。

A. 相关工作

1）可通行性分析（Traversability Analysis）：地形是否适合导航可以通过多种方式进行评估，例如基于本体感测（proprioceptive）测量[23][24]、几何特征[1][2][25]，以及几何与语义特征的结合[3][4][26]（详见综述文献[27]）。由于难以基于地形特征手工设计规划代价，自监督学习正越来越多地被用于学习与任务相关的可通行性表示。例如，Li 等人[28]提出了一种在密集植被下学习支撑面的方法，用于腿式机器人的行走；Gasparino 等人[21]建立了一种地形牵引力模型，用于表示机器人在执行期望速度指令时的跟踪能力。然而，这些方法并未考虑由于真实世界数据的噪声性和稀缺性所带来的非确定性（uncertainty），即Aleatoric 不确定性和Epistemic 不确定性。为捕捉 Aleatoric 不确定性，Ewen 等人[10]与 Cai 等人[11]利用高斯混合模型或分类分布学习了多模态地形属性。为捕捉 Epistemic 不确定性，Frey 等人[12]与 Schmid 等人[13]评估了训练好的神经网络在重构过去 traversed 地形方面的能力，Seo 等人[29]则训练了一个用于识别陌生地形的二分类器。相比之下，Endo 等人[15]与 Lee 等人[14]使用高斯过程（Gaussian Process, GP）回归来量化 Epistemic 不确定性，但他们假设噪声方差在全局是恒定的，即采用同方差（homoscedastic）噪声模型。Murphy 等人[30]虽然采用了异方差（heteroscedastic）GP，可处理输入依赖的噪声，但其预测分布在解析上不可求解，因此需依赖近似方法。

与之相对，我们的工作在学习牵引力模型的同时，显式地量化了 Aleatoric 与 Epistemic 不确定性。该模型预测的是实际速度与命令速度之间的比值。虽然我们也像 Gasparino 等人[21]那样学习牵引力模型，但我们的方法是具备不确定性感知能力的，并可用于实现风险感知的导航（risk-aware navigation）。相比之下，Frey 等人[12]虽在规划目标中使用了实际速度与指令速度的差异，但在进行状态预测时假设无打滑（no slip）。而我们的牵引力模型可以用于在最差期望牵引力条件下模拟状态演化（state rollouts），实验结果表明，这一策略在性能上优于那些假设名义牵引力的传统方法。

2）不确定性量化与 OOD 检测（Uncertainty Quantification and OOD Detection）：不确定性量化在机器学习领域已有广泛研究（详见综述文献[31]），其中包括一些有效技术，如 Bayesian Dropout[32]、模型集成（Model Ensembles）[33] 和证据方法（Evidential Methods）[34]。在越野导航的相关研究中，模型集成方法被广泛采用[35][36][37]，因为它们通常优于基于 Bayesian Dropout 的方法[38]。相比之下，证据方法更适合实际部署场景，因为它们仅需单次网络前向计算，不会带来过高的计算或内存开销。因此，我们采用了 Charpentier 等人[16]提出的证据方法，通过神经网络输出直接参数化目标分布的共轭先验分布，从而同时量化 Aleatoric 和 Epistemic 不确定性。此外，我们提出了一种基于 Hou 等人[19]提出的平方形式的地球移动距离（Squared Earth Mover’s Distance, EMD）的不确定性感知损失函数，能够更好地捕捉离散牵引力值之间的关系，从而提升牵引力预测的精度，进而提高后续风险感知规划器的导航性能。 在部署训练好的牵引力模型时，我们通过估计得到的 Epistemic 不确定性显式识别 OOD（Out-of-Distribution）地形，这属于通用 OOD 检测问题的一种实例（综述见[39]）。例如，Seo 等人[40]采用的基于重构的方法，以及 Ancha 等人[41]采用的基于密度的方法，均在越野导航中展示了识别危险地形的良好效果。与 Ancha 等人[41]类似，我们的方法是一种基于密度的方式，通过学习训练数据分布下的标准化概率密度显式建模。作为替代，Liu 等人[42]与 Grathwohl 等人[43]提出的基于能量的方法（Energy-based Approaches）无需显式密度归一化，类似的思想也被 Castaneda 等人[44]用于避免进入 OOD 状态。不同于只关注 OOD 检测与规避的方法，本研究同时量化并缓解 Aleatoric 与 Epistemic 不确定性带来的风险。虽然在测试阶段应尽量规避高 Epistemic 不确定性的 OOD 地形，但分布内的地形（in-distribution terrain）仍可能由于复杂的车-地交互导致预测牵引力具有较高的 Aleatoric 不确定性。因此，需要独立处理由 Aleatoric 不确定性引起的风险，使机器人能够在低牵引力风险与节省时间之间进行权衡，以提升整体导航性能。

3）风险感知规划（Risk-Aware Planning）：在地形通行性存在不确定性的情况下，通行风险可通过代价地图（costmaps）来表示。例如，Fan 等人[45]和 Triest 等人[35]使用代价地图，其中引入条件风险值（Conditional Value at Risk, CVaR）来衡量遇到最坏情形期望失败的代价。CVaR 满足一组对理性风险评估非常关键的公理条件[46]。除代价地图外，导航性能也可以基于期望未来状态（Gibson 等人[47]）或期望牵引力值（Gasparino 等人[21]）来评估。然而，这些方法依赖于名义系统行为或期望系统行为，在车辆与地形之间存在显著噪声（即 Aleatoric 不确定性较高）时，往往难以准确反映真实性能。作为替代方案，Wang 等人[22]提出直接优化规划目标的 CVaR，其方法是通过对不确定参数采样，并在每条控制序列上进行评估来估计 CVaR，但这种方法计算开销很大。与我们的方法类似，Lee 等人[36]近期的工作使用概率集成方法（probabilistic ensembles）[48]同时量化 Aleatoric 和 Epistemic 不确定性，并通过对这两类不确定性加权惩罚，实现风险感知的轨迹规划。但他们的方法仍依赖于期望系统行为。

与其类似，我们也通过辅助惩罚项来处理 Epistemic 不确定性，但在处理 Aleatoric 不确定性时，我们采用最坏情况下的期望系统参数进行前向仿真，以评估风险。这种方式相比 Wang 等人[22]提出的采样方法在计算上更加高效；相比 Lee 等人[36]与 Gasparino 等人[21]基于期望系统行为的方法，我们的方法在面对现实中存在多模态地形属性时表现出更强的鲁棒性。

B. 本文贡献

我们提出了 EVORA：一个面向越野导航的完整流程，将不确定性感知的可通行性学习问题与风险感知的运动规划问题紧密集成。我们显式地量化了两类不确定性：Epistemic 不确定性：用于识别在陌生地形下牵引力预测不可靠的情形；Aleatoric 不确定性：用于支持下游规划器缓解由噪声牵引力估计引起的风险。本文的主要贡献如下：

1）一个基于牵引力分布的概率可通行性模型，用于建模 Aleatoric 不确定性，并通过预测器潜特征的密度来识别预测结果是否可靠（从而量化 Epistemic 不确定性）。

2）提出一种新颖的、不确定性感知损失函数：基于平方形式的 EMD 损失（EMD² loss，[19]）并由本文推导出封闭形式表达。与不确定性感知交叉熵损失（Uncertainty-aware Cross Entropy, UCE，[16]）联合使用时，该损失可提高牵引力预测精度、OOD 检测性能，以及下游导航性能。

3）设计一个基于牵引力 CVaR 的风险感知规划器，用于处理 Aleatoric 不确定性。实验表明，该规划器优于仅假设名义牵引力[11]或期望牵引力[21]的方案，并在仿真与真实硬件测试中，性能超过或可与优化代价 CVaR 方法[22]相媲美。

4）对上述风险感知规划器进行扩展，使其能够处理 Epistemic 不确定性，即通过规避 OOD 地形来提高仿真中的导航成功率，并在硬件实验中减少人工干预次数。

本工作的初步会议版本发表于文献[49]，当时提出了学习牵引力分布并使用牵引力 CVaR 进行规划的方法。而本篇扩展工作在以下方面进行了改进：采用文献[16]提出的证据学习方法（Evidential Learning）进行模型训练；基于文献[19]推导新的 不确定性感知的 EMD² 损失函数，显著提升了学习效果。这些新方法不仅提升了牵引力预测精度与 OOD 检测性能，还带来了更快的导航速度。通过增加大量硬件实验，本文进一步验证了会议版本[49]中所提出的风险感知规划器相比当前最先进方法[11][21][22]的性能提升。

Ⅱ 问题概述

我们考虑的问题是：在地形牵引力影响下，地面机器人如何实现快速导航至目标点。由于牵引力值具有不确定性，我们在第 II-A 节中引入了以牵引力为随机变量的动力学模型；在第 II-B 节中引入了以“到达目标所需时间”为指标的规划目标函数；并在第 II-C 节中讨论了最小化该时间目标所面临的挑战。

A. 含牵引力参数的动力学模型

考虑以下离散时间系统：

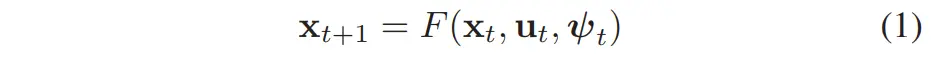
其中：：机器人状态向量（如位置与朝向）；：控制输入（例如线速度与角速度）；：用于描述地形牵引力的参数向量。我们考虑两种可近似多类机器人动力学行为的模型，如图 3 所示。

图 3.可以用独轮车或自行车建模的地面机器人示例动力学模型。（a） 遥控车。（b） 差动驱动机器人。（c） 腿式机器人。 

1）单轮车模型（Unicycle Model） 

适用于差速驱动机器人与腿式机器人，定义如下：

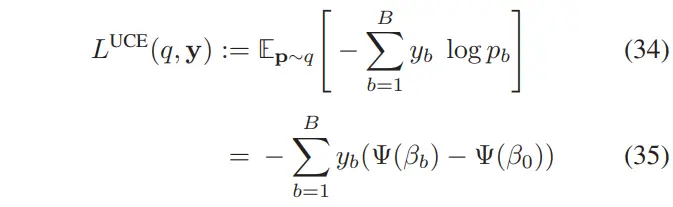
其中：：位置和航向角；

：命令的线速度和角速度；

：线向与角向的牵引系数（范围）；

：时间步长。

直观理解：牵引力表示滑移程度，即实际速度与命令速度的比值。

2）自行车模型（Bicycle Model） 适用于阿克曼转向机器人，定义如下：

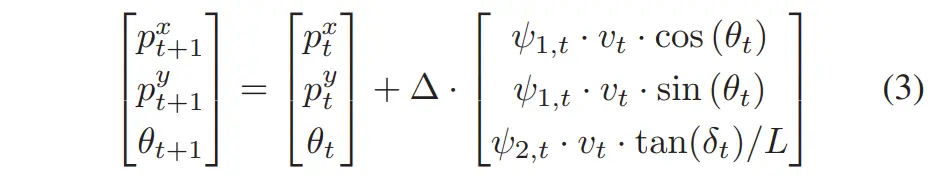
其中：：车轮轴距；

：命令的线速度和转向角；

：含义同上，用于建模不同方向的牵引比例；

参考点：为后轮轴中点。

B. 规划目标

我们采用文献 [11] 中提出的最短时间目标函数（minimum-time objective），当然也可以采用其他形式的“到达目标”类目标函数。直观地说，该目标函数在系统状态尚未进入目标区域之前，通过累加时间步来施加阶段代价（stage cost）。如果状态轨迹从未到达目标区域，则还会施加一个终端代价（terminal cost），以惩罚估计的剩余时间。

设有函数 用于计算当前状态 与目标之间的欧氏距离，则从时间  到  的状态轨迹  上的最短时间目标函数定义为：

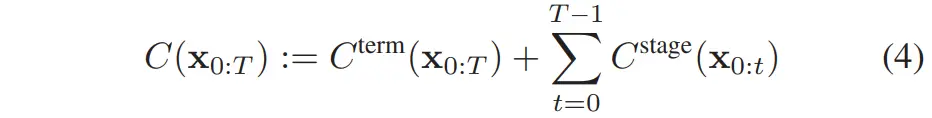
即总代价由终端代价和阶段代价两部分组成。

终端代价和阶段代价定义为：

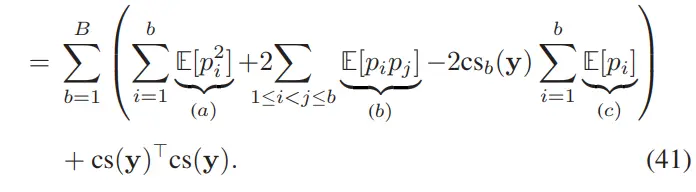
其中：：用于估计剩余时间的默认速度；

：固定的时间间隔；

：指示函数，若轨迹  中存在某个状态已到达目标区域，则取值为 1，否则为 0。

我们使用该指示函数来避免在到达目标后继续累计代价。尽管时间间隔 是固定的，但实际达到目标所需的步数取决于机器人在不同地形条件下的实际速度。从直觉上来看，该目标函数的设计旨在鼓励机器人尽可能快地到达目标区域。

C. 关键挑战

虽然目标函数（公式（4））可以通过非线性优化方法（如 模型预测路径积分控制（Model Predictive Path Integral, MPPI），参见文献 [18] 中的算法 2）来寻找最优控制序列以实现优化，但地形牵引力在不同地形类型之间存在变化，因此必须从真实环境中进行学习。然而，现实世界中的地形牵引力存在不确定性：一方面，即使是外观和几何特征相似的地形，其牵引力性质也可能差异显著，属于Aleatoric 不确定性；另一方面，牵引力模型的训练只能依赖于有限的数据集，这会导致Epistemic 不确定性。即使我们能够对地形牵引力的不确定性进行准确建模，如何设计一个在该不确定性下仍能降低失败风险的风险感知规划器仍然是一个重大挑战。为应对这些挑战，我们在第 III 节和第 IV 节分别提出了不确定性感知的可通行性模型与风险感知的规划器。

Ⅲ 不确定性感知的可通行性建模

在本节中，我们首先介绍一个用于建模Aleatoric 不确定性的牵引力分布预测器（traction distribution predictor），以及一个用于建模Epistemic 不确定性的潜空间密度估计器（latent space density estimator）。整套可通行性分析流程如图 4 所示。随后，我们在牵引力学习的背景下回顾文献 [16] 提出的证据学习方法（evidential method），并进一步提出一种新的不确定性感知损失函数，以提升学习性能。

图 4.提出的可遍历性管道将海拔和语义特征映射到捕获随机不确定性的牵引分布，以及捕获认识不确定性的潜在特征的密度。如果潜在要素的密度低于阈值，则 Terrain 区域被视为 OOD，稍后在规划期间会避免使用。当潜在特征的密度高于阈值时，预测的牵引力分布是可靠的，并通知下游风险感知规划者（第 IV 节）在固定风险与牵引不确定的穿越区域所节省的时间之间进行权衡。

A. Aleatoric 不确定性：牵引力分布建模

设：为一个包含  个离散牵引力取值的集合（这些取值表示实际速度与指令速度的比值）； 为地形特征的集合，其中包含高程值以及地形语义标签的 one-hot 向量表示。我们的目标是：在输入地形特征向量的条件下，对牵引力空间 建模其分布：

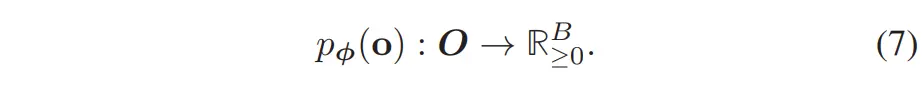
我们用 表示定义在  上的分类分布（categorical distribution），该分布反映了由于环境因素导致的Aleatoric 不确定性（即影响牵引力但在特征 中无法显式表达的因素）。需要注意的是，公式（7）中的分布可以通过一个由参数  控制的神经网络（NN）来建模，并通过经验数据集进行训练。该数据集形式为：虽然我们没有显式建模地形特征本身的不确定性（例如：高程估计噪声、因外观相似导致的语义标签误判）或其他因素（如低层速度控制器的设计），但这些未建模因素将反映在实际采集的数据中，并能通过训练牵引力分布间接体现。

我们采用分类分布（categorical distributions）来作为高斯混合模型（Gaussian Mixture Models, GMMs）和正态化流（normalizing flows，[17]）的可行替代，用于学习实际中出现的多模态牵引力分布，原因如下：分类分布无需手动调节簇数量；天生构造出有界分布（bounded distributions）；根据我们的经验，其收敛速度快于 normalizing flows，且在精度上可达到相近水平。由于我们仅需对 一维的线向与角向牵引力值进行离散化，因而避免了在高维空间中离散化导致的指数级增长的问题。因此，采用有限数量的离散 bin 的分类分布就足以满足任务需求。

图 5. 数据采集与离线数据集生成流程。(a) 使用 Clearpath Husky 机器人进行真实环境数据采集的示意图。机器人在人工驾驶下行驶约 10 分钟，同时记录其路径轨迹、牵引力值，并构建环境的语义地图与高程图。牵引力值以 20 Hz 频率记录。图中为清晰起见仅展示了部分牵引力数据，其中牵引力值出现不连续的位置对应于未发送线速度或角速度命令的时刻。(b) 离线数据集生成阶段，牵引力值被离散化后，按遍历路径中的地图单元格累计为直方图形式存储。牵引力预测器的输入由语义 patch 和高程 patch 组成。地形类别示例包括：植被（浅绿色）、草地（深绿色）、裸土（浅棕色）、覆盖物/腐殖层（深棕色）。预测牵引力分布与经验牵引力分布用于计算训练损失，而生成经验牵引力分布所用的测量计数可用于对训练损失加权，从而降低对少见地形区域的过拟合风险。(a) 数据采集流程。(b) 离线数据集生成流程。

图 5 展示了真实数据采集与离线数据集生成的示例。环境的语义与几何信息可以通过 语义 OctoMap（semantic octomap，[50]）构建，该方法通过时间融合语义点云来获得三维结构。我们使用 PointRend[51] 对 RGB 图像进行分割，该网络在 RUGD 越野导航数据集[52] 上进行过训练，支持 24 个语义类别。分割结果随后会被投影到激光雷达点云上，从而将语义信息转移到空间地图。在离线数据集生成阶段，我们通过将牵引力值离散后累计为直方图的方式，得到经验性线向与角向牵引力分布。这些直方图分别存储在机器人遍历过的每一个地形单元格中。同时，我们也存储每个单元格内的测量次数，以便在训练过程中按照这些计数对损失函数加权，从而降低在稀疏地形上因样本稀少导致的不稳定学习影响。在实际操作中，我们分别学习线向与角向牵引力分布。神经网络的架构如下：一个共享编码器（shared encoder），包括卷积层（CNN）和后续的全连接层，用于同时处理地形的语义与高程 patch；编码器之后接两个独立的全连接解码器头部（decoder heads），分别用于预测线向与角向牵引力分布，每个输出采用 softmax 激活函数。

B. Epistemic 不确定性：潜空间密度建模

由于训练数据有限，牵引力分布预测器在遇到新颖地形区域时的输出可能不可靠，从而导致该区域的导航性能下降。为了度量这种 Epistemic 不确定性，我们希望估计牵引力预测器中某个中间层提取出的潜特征 的密度，该特征是基于地形输入特征 得到的。密度估计器定义如下：

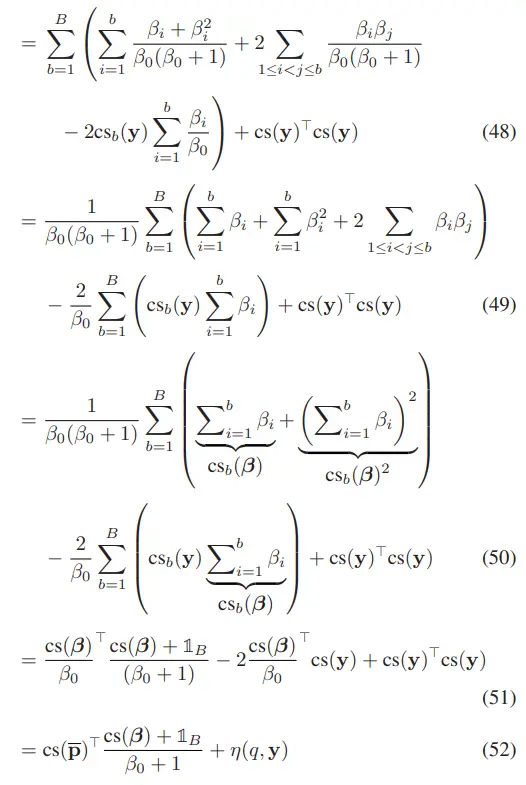
我们使用一个由参数  控制的正态化流模型（normalizing flow）来学习上述密度函数。从整体上看，正态化流的原理是：通过一系列可逆且可微的映射函数，将目标分布（如潜空间分布）变换为一个简单的基础分布（base distribution），例如标准正态分布。然后，使用变量变换公式（change of variable formula，[17]），可以计算任意样本的密度：其密度为：变换后样本在基础分布上的密度值；变换函数的Jacobian 行列式的绝对值（即体积变化因子）的乘积。在选择潜空间特征时，必须确保该特征包含与任务相关的信息。为此，我们使用由共享地形特征编码器（shared terrain feature encoder）产生的潜特征，因为该编码器同时用于预测线向与角向牵引力分布，其表示能力足够强。 

为了更直观地使用密度作为不确定性指标，我们设计了一个简单的置信度函数 ，用于衡量输入特征  的置信程度。该函数基于训练集内所有地形样本的潜空间密度分布中观察到的：最大密度 ；最小密度。该置信度可用于规划中区分训练内分布（in-distribution）与 OOD 地形（out-of-distribution terrain）。

在部署阶段，若某地形特征的置信度得分低于某个设定的门限 ，则认为该地形为 OOD（Out-of-Distribution）。此类具有 OOD 特征的地形区域可以在路径规划中通过辅助惩罚项（auxiliary penalties）显式规避。一个较为系统的设定方式是：将 设为训练集中所有地形特征的潜特征密度的第  分位数（percentile），即：；较高的值意味着测试时更多地形将被归为 OOD。由于在公式（9）中使用了归一化操作，选择和 分别对应训练集中密度的第 0 百分位（最小值）与第 100 百分位（最大值），这为门限选择提供了便利。值得注意的是，这个门限可以离线选定，例如若希望机器人仅规避密度低于训练集最小值的区域，可以简单地设置。这种策略在部署牵引力预测模型于训练外场景时（即未见过的新地形），能够显著提高导航成功率。这一效果在仿真实验（见第 VIII 节）与真实硬件实验（见第 IX-B 节）中均得到了验证。

C. 证据深度学习

尽管牵引力预测器与密度估计器可以采用顺序训练（sequential training）方式分别训练，但 Charpentier 等人 [16] 证明了：基于证据深度学习（evidential deep learning）的联合训练能够在保持预测精度的同时，显著提升 OOD 检测性能。本节中，我们回顾文献 [16] 提出的训练方法与损失函数。在该方法中，神经网络的输出参数化了一个 Dirichlet 分布，该分布是分类分布（categorical distributions）的共轭先验。

设  表示一个 Dirichlet 分布，其浓度参数为：，这是定义在 个 bin 上的一个层级概率分布，其中下层的分类分布  的参数  满足：即 p 是一个归一化的概率质量函数（PMF），它由上层的 Dirichlet 分布生成：Dirichlet 分布的期望（即期望 PMF）为：该期望 PMF 表征了 Aleatoric 不确定性。Dirichlet 分布参数的总和：表示分布相对于其期望的集中程度（concentration），也称为总证据量（total evidence）。证据越高，表示 Epistemic 不确定性越低，因为该样本在训练集中观察得更多。给定一个先验 Dirichlet 分布 ，神经网络会基于输入特征  执行一次输入相关的后验更新，从而学习出对该输入的置信表达。

后验 Dirichlet 分布 同时依赖于：由牵引力预测器 （见公式（7））预测的牵引力分布；与潜特征密度 （见公式（8））成比例的预测“证据” ；一个预设的置信预算常数 。由此可得，后验 Dirichlet 分布对应的期望牵引力 PMF 为：

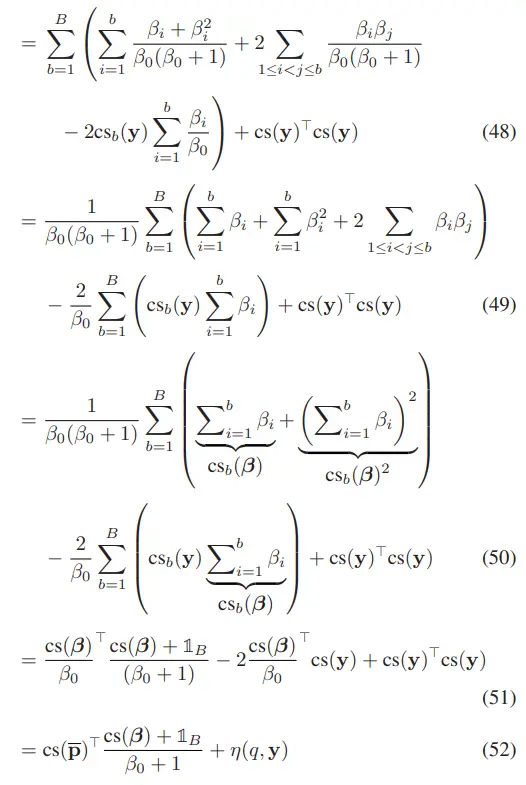
其中：：先验 Dirichlet 分布的总浓度；先验分布的期望 PMF。我们采用平坦先验（flat prior），令： 其中 为全 1 向量，从而得到一个在所有可能 PMF 上均匀的 Dirichlet 分布。基于文献 [16] 的该建模框架，后验 Dirichlet 分布 及其期望牵引力分布 都依赖于牵引力预测器、潜密度估计器与输入地形特征。为了简化符号，下面对损失函数的分析中将统一使用一般形式的 Dirichlet 分布  与 。但在实际训练中，应将它们替换为上述的（后验形式）公式（10）、（11）、（12）。 

给定一个目标概率质量函数（PMF）向量 ，其表示通过经验数据估计得到的牵引力分布，我们可以将牵引力预测器和 normalizing flow 模型联合训练，使用以下的 UCE（Uncertainty-aware Cross Entropy）损失函数 [16]：

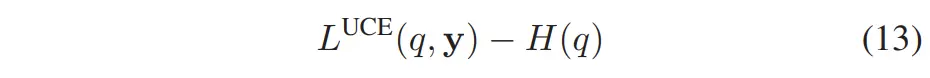
其中：≔是期望交叉熵损失（expected CE loss），而  是一个用于鼓励分布平滑性的熵正则项。需要注意的是， 和  都依赖于 Dirichlet 分布的参数 （详见附录 A）。 文献 [16] 中的消融研究表明，使用上述损失（公式 (13)）进行训练，在保持传统交叉熵损失精度的同时，能够有效提升 OOD 检测性能。然而，CE 类损失函数在本研究中的一个关键缺陷在于：它将所有 bin 之间的预测误差视为相互独立。这种“独立性假设”在牵引力建模场景中并不合理，因为：所有 bin 是通过对连续牵引力值进行离散化获得的；这些 bin 是有序的——即，距离较近的 bin 在语义上应当比距离较远的 bin 更为相似。为了解决这个问题，我们提出了一种新的损失函数，基于平方地球移动距离（squared Earth Mover’s Distance, EMD²） [19]。已有研究表明，在 bin 有序的情形下，该损失相比基于交叉熵的损失可获得更好的预测精度。

D. 不确定性感知的平方地球移动距离

直观上，EMD（Earth Mover's Distance） 衡量的是：将一个分布的概率质量转换为另一个分布所需的最小“运输代价”。对于两个具有相同数量 bins 的分类分布（categorical distributions），EMD 可以计算为封闭形式解 [19]。给定一个预测的概率质量函数（PMF）  与目标 ，在 bin 等间距的前提下，基于 ℓ-范数的归一化 EMD 可写为：

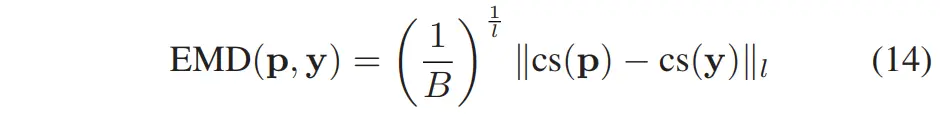
其中：表示累加求和（cumulative sum）操作；实际训练中，我们令，即使用欧氏距离（Euclidean distance）；并优化其平方形式损失函数，记作 EMD²，省略了乘法常数项。图 6 中的示例清楚地表明：与忽略 bin 间关系的交叉熵（CE）相比，EMD² 能更好地表达预测 PMF 的物理含义。

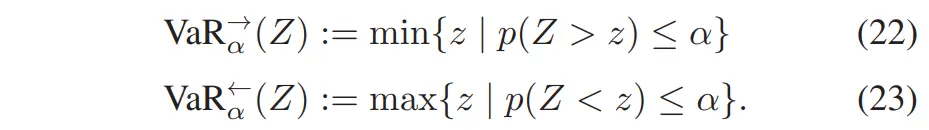
图6. EMD2和CE之间的差异。给定真实值（GT）和预测值和，CE产生相同的值，而EMD2对的惩罚更大。实际上，EMD²更为理想，因为它考虑了离散化的牵引值之间的跨区间关系。

由于 EMD² 仅定义在 PMF 上，一个朴素但有效的策略是：将目标分布  与 Dirichlet 分布 的期望 PMF 进行比较。从而定义如下损失函数（忽略常数乘子）：

其中：≔是 Dirichlet 的期望 PMF；≔ 是总证据量（total evidence）；定义为：

由于累计和操作具有线性性质，因此：因此，是与总证据量 无关的，这意味着它对 Epistemic 不确定性（由证据控制）的学习并不敏感，如图 7 中的示例所示，因此无法有效学习 Epistemic 不确定性。

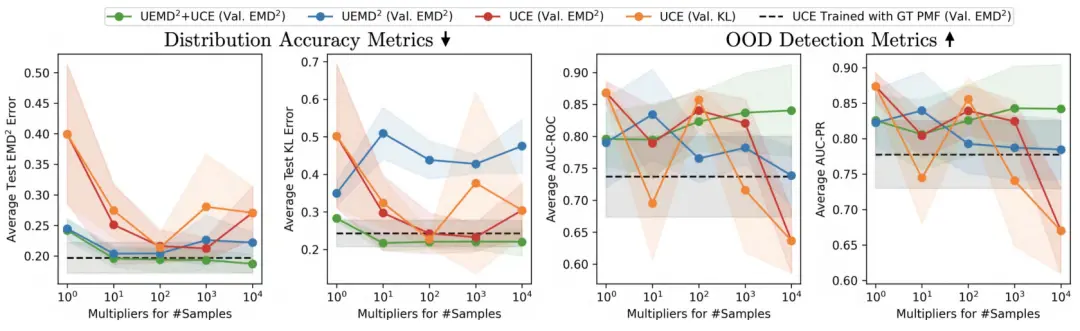
图 7. 在一个包含三个分箱、、 的简单示例中，分析标准 EMD² 损失与我们提出的 UEMD2 损失之间的差异。每个蓝色三角形表示预测的狄利克雷分布 ，可视化为 3-单纯形上的概率密度；单纯形内的每个点对应三个分箱上的分类分布。红色十字 + 表示目标标签分布  在训练集中的位置。狄利克雷分布可以通过两个量进行参数化：其均值的位置及其在均值附近的集中度。左图：在保持狄利克雷分布集中度不变的情况下，改变其位置。在这种情况下，两种损失的行为相似且符合预期——它们促使预测的狄利克雷分布接近目标标签分布。右图：在保持狄利克雷分布集中度不变的情况下，改变其在类集 (GT) 上的位置。由于 EMD² 仅取决于狄利克雷均值的位置，因此它相对于变化的集中度而言是恒定的。然而，我们提出的 UEMD² 鼓励预测的狄利克雷函数具有较高的集中度（低认知不确定性）。学习预测分布内训练样本的低认知不确定性对于校准不确定性预测和检测 OOD 样本至关重要，而不是对集中度漠不关心。

 类似于文献 [16] 中基于 的交叉熵期望损失定义方式，我们提出了不确定性感知平方地球移动距离（UEMD²）损失，将其定义为预测的 Dirichlet 分布  下的 EMD² 期望：

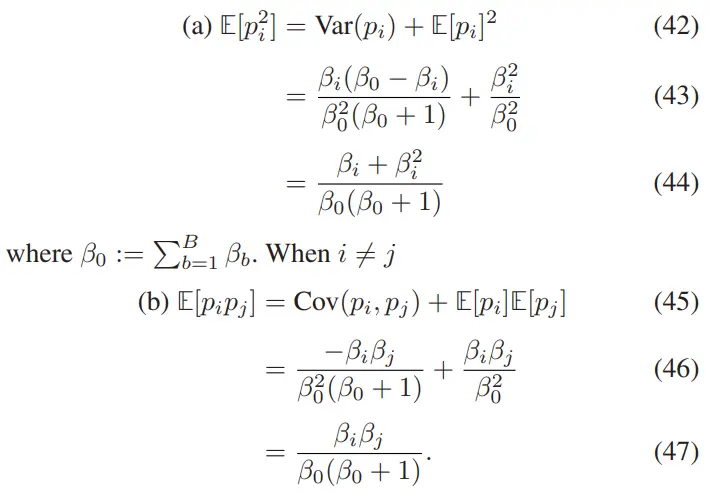
我们提出的 UEMD² 损失具有封闭形式，如下定理所示：

定理 1：令 为一个 Dirichlet 分布，为一个分类目标分布，则其期望  损失函数具有如下闭式表达：

其中：≔： 定义见公式（16）。

证明：见附录B。

由于与公式（15）中的 在结构上的相似性，式（18）同样惩罚预测 PMF 的 EMD² 误差，从而提升牵引力预测精度。此外，式（18）还包含了对 Dirichlet 总证据量 的反向惩罚项，从而有效鼓励模型输出集中度高（低 Epistemic 不确定性）的预测，如图 7 所示。事实上，可以证明（利用 Jensen 不等式与 的凸性）：虽然 UEMD² 损失可单独用作损失函数，但其平方项特性有时会导致训练停在非期望的局部最优 [19]。为此，我们参考文献 [19]，引入一个联合损失函数，融合了 CE 和 EMD² 的优势，定义如下多目标优化目标：

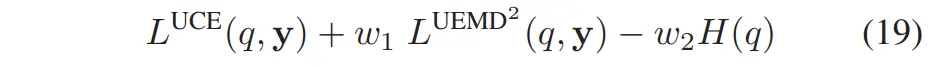
其中：：Dirichlet 分布的熵，鼓励分布光滑；：超参数，用于调节各项损失的重要性。在实践中，我们对预测的线向与角向牵引力分布分别计算公式（19）中的总损失，然后进行平均。如第五节第 C 小节（Section V-C）中的仿真结果所示，该多目标损失函数（19）相比单一损失，训练更稳定，且在测试阶段具有更好的泛化能力。

Ⅳ 基于学习牵引力分布的风险感知规划

尽管应规避那些可能导致 高 Epistemic 不确定性 的 OOD 地形，但在分布内（in-distribution）的地形上，由于复杂的车-地相互作用，仍可能引发 高 Aleatoric 不确定性，从而造成牵引力不稳定。因此，我们提出了一种风险感知的规划器（risk-aware planner），能够权衡以下两者之间的关系：失去动力（immobilization）的风险；在高不确定性地形上通行所带来的时间节约潜力。

A. 条件风险值

我们采用 CVaR（Conditional Value at Risk） 作为风险指标，因为它满足一组用于理性风险评估的重要公理 [46]。传统 CVaR 定义假设风险位于分布右尾（right tail），而我们对随机变量 ZZ 在给定风险水平 下，分别定义其左右尾的 CVaR（见图 8）如下：

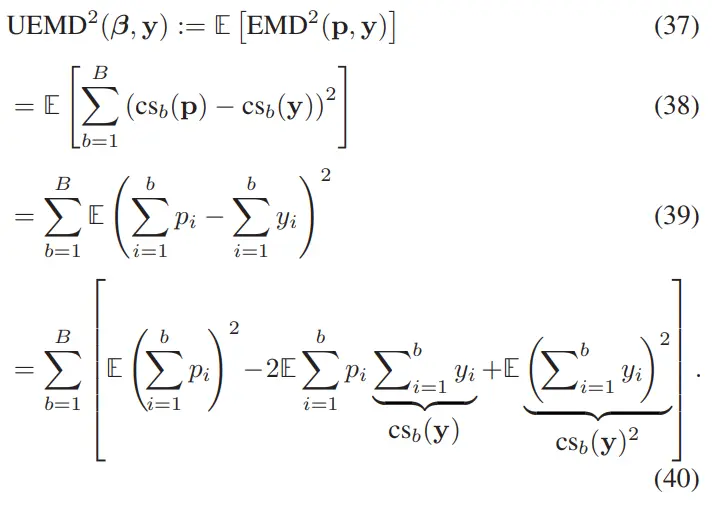
图 8. 本研究定义了两种条件风险价值（CVaR）的版本，以捕捉随机变量 (  ) 在左尾或右尾的最坏情况期望值，分别为 (  ) 和 ( )，其中最坏情况构成了总概率的 ( ) 部分。左尾和右尾的风险价值（VaR）分别定义为 (  ) 和 (  )。

其中，左右尾的 VaR（Value at Risk）定义如下：

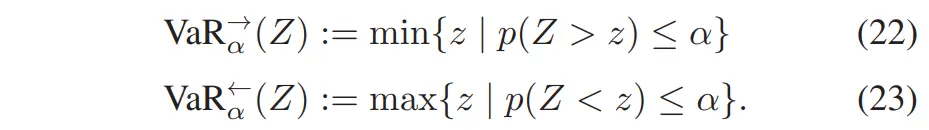
从直观角度理解： 和 分别衡量右尾与左尾区域的期望结果；每个尾部所占概率质量均为 ；通常，右尾用于衡量需要最小化的代价（如时间、能耗）；左尾用于衡量低牵引力情形的风险，更适用于越野可通行性问题。

当  时，左右尾 CVaR 定义均等价于期望值：

B. 风险感知规划

为应对因牵引力不确定性带来的风险，我们首先介绍文献 [22] 提出的基线方法：该方法优化规划目标函数的右尾 CVaR（CVaR-Cost）。随后，我们提出一种计算效率更高的方法，即基于牵引力左尾 CVaR 的成本设计（CVaR-Dyn）。最后，我们分析这两种方法的优缺点。

1)最坏情形期望代价（CVaR-Cost [22]） 给定初始状态 ，我们希望找到一个控制序列 ，使得在地形牵引力不确定的情况下，最小化名义代价函数 （公式 (4)）的右尾 CVaR：

其中：牵引力是从预测的牵引力分布（公式 12）中采样得到；由于牵引力不确定，变为一个随机变量，依赖于状态轨迹的实现过程。该方法受到文献 [22] 的启发，但我们进一步支持与地形特征相关的牵引力分布建模。

在实际中，优化问题（24）可通过 MPPI（Model Predictive Path Integral） 实现，方法是对每个控制序列生成  个牵引力样本，并估计其对应的 CVaR 值：为加速训练，可利用 GPU 并行预生成  张牵引力图，每张图中每个地图单元格存储一个牵引力样本，从而使每组控制序列可在所有图上并行评估。但随着地图尺寸增加，计算开销仍会迅速膨胀。

2)最坏情形期望牵引力（CVaR-Dyn）

为提高计算效率，我们提出一种新方法：使用地形牵引力分布的左尾 CVaR来替代 Monte Carlo 采样。目标是最小化名义代价函数 C，但轨迹是由最坏情形牵引力决定的：

当  时， 等价于期望值，即退化为文献 [21] 所采用的方法。

3)优点与局限性（Advantages and Limitations）

CVaR-Cost 与 CVaR-Dyn 都建立在“最坏情形”风险的直觉之上，分别使用：CVaR-Cost：目标函数的 CVaR；CVaR-Dyn：牵引力参数的 CVaR。它们的优势：所有地形类型共享一个风险参数 ，调参简单；CVaR-Cost 是更一般性的风险处理方法（但计算复杂）；CVaR-Dyn 计算效率更高，更适合大规模地图。CVaR-Dyn 的局限在于：其直觉假设“低牵引力 → 时间更长”并非总成立；对于更复杂系统和目标函数，可能不适用。

Ⅴ 可通行性学习管线的评估

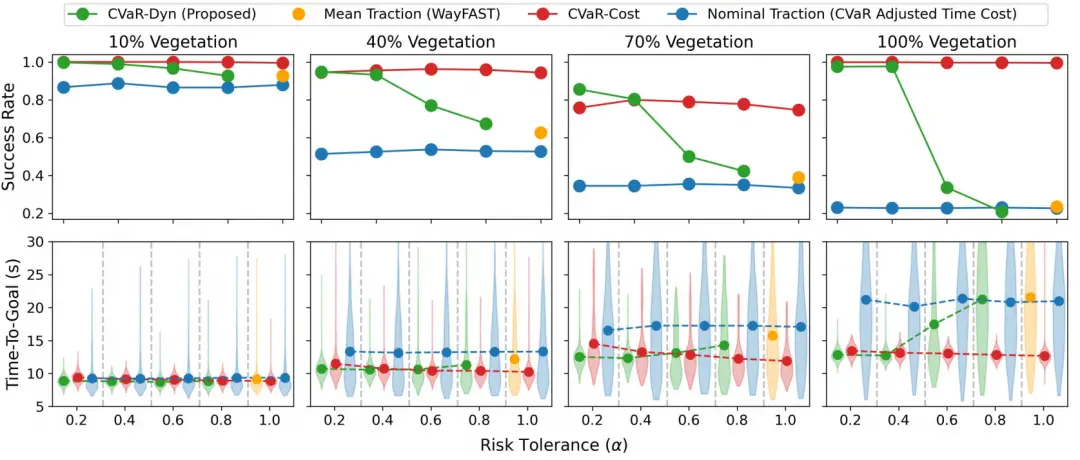
我们提出的 证据式可通行性学习方法（evidential traversability learning method） 在一个合成地形数据集上进行评估（见第 V-A 节）。该数据集被设计为模拟真实环境下数据稀缺的情况，提供牵引力的真实值（GT traction distributions）和 OOD 地形掩码（OOD terrain masks）。我们比较了多个损失函数变体（如公式 (19)），在预测精度与 OOD 检测性能（见第 V-C 节）上的表现。为突出联合训练与 UEMD² 损失（公式 (18)）的优势，我们还在第 V-D 节进行了消融实验。分析完第四节的规划器后，第六节将介绍系统的组成方式，第七节展示了我们损失函数对导航性能的提升效果。尽管不确定性量化本身并非本文重点，我们建议读者参考文献 [16]，其中详细探讨了本文所用神经网络架构在学习精度、OOD 检测能力和计算效率上相较其他先进方法的优势。

A. 合成三维地形数据集

我们使用的合成数据集包含随机生成的 3D 地形，对应的 GT 牵引力分布依据地形的几何属性（如坡度、高程）与语义类别（如泥土与植被）生成，具体定义详见表 I。注意：坡度仅用于生成牵引力 GT，不作为神经网络的输入。为简化问题，线向与角向牵引力使用相同分布；依赖关系只存在于：泥土类型与地形坡度之间；植被类型与地形高程之间。尽管可以设计更复杂的牵引力函数，我们提供的数据集已足以支撑本文工作。

表 I 用于基准测试损失函数的合成地形数据集

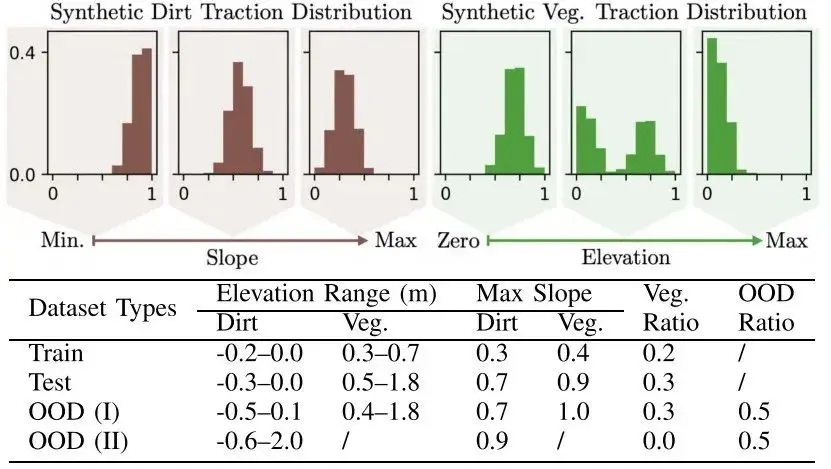
GT（真实）牵引分布针对泥地为单峰高斯分布，其均值随地形坡度增加而增大，反映地形的崎岖程度。植被的牵引分布基于海拔高度：在中等海拔时呈双峰分布，在最低和最高海拔时为单峰分布。需注意，OOD 数据集（I）包含混合地形类型，而OOD（II）则不含植被，以确保学习到的模型不单纯依赖语义信息进行 OOD（分布外）检测。

具体构成如下：5 个训练环境、20 个测试环境、40 个 OOD 环境；每个环境大小为 30×30 米，分辨率为 0.5 米；参数变化包括：高程、坡度、植被比例。为了模拟模型泛化能力，训练集特意保持较小规模。每个训练环境再细分为训练集与交叉验证集。图 9 展示了合成环境的部分可视化结果。为模拟真实世界的数据采集：牵引力样本仅沿圆形路径采集；为分析数据量对学习的影响，我们通过将测量样本数乘以 , 来扩展训练数据量。

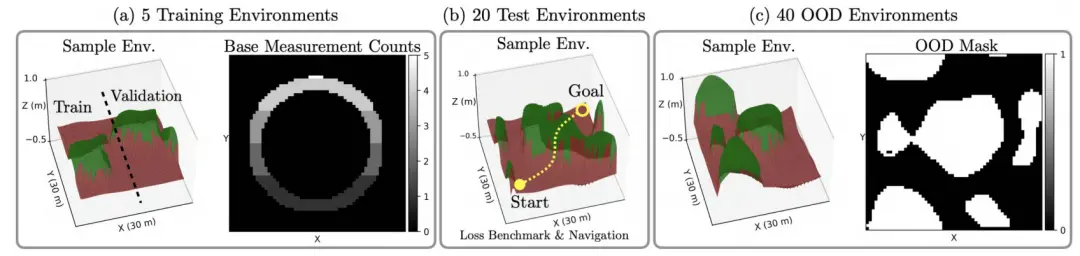
图 9. 包含泥土（棕色）和植被（绿色）语义类型的合成三维地形数据集。(a) 在每个训练环境中，沿着预设的圆形路径进行有限的牵引力测量，以模拟有限覆盖范围内的真实世界数据收集。每个环境被分成两个进行交叉验证。此外，我们通过将基准测量计数相乘来分析不同测量次数的影响（见图 10）。(b) 测试环境包含用于分析牵引力预测精度的新型地形特征。为了支持EMD² 是更好的导航性能指标这一关键论点，在测试环境中部署了使用不同损失函数训练的模型，用于执行“前往目标”任务（见第七节）。(c) 与测试环境相比，OOD 数据集还为训练期间未观察到的高程和/或坡度的新型地形提供了二值掩码。(a) 训练环境示例。(b) 测试环境示例。(c) OOD 环境示例。

在训练环境中：通过直方图统计记录牵引力分布，并记录每个terrain cell 的采样次数，以在训练时加权损失函数；在测试环境中：使用 GT 分布评估预测精度；在 OOD 环境中：坡度与高程值未在训练中出现者被视为 OOD；OOD 掩码作为 GT 标签用于 OOD检测性能评估，图 9(c) 展示其示例。

B. 模型训练

我们对所有损失函数使用相同的神经网络结构：牵引力预测器由一个共享编码器（卷积层 + 全连接层）组成，用于处理语义与高程图 patch；其后接两个 全连接解码头，分别输出线向与角向牵引力分布的 softmax 概率。从共享编码器得到的潜特征被送入一个径向流（radial flow）模型 [53]。为数值稳定起见，我们使用一个固定的置信预算，其值随潜空间维度以指数增长 [16]。训练采用 [16] 提出的两阶段流程：联合训练牵引力预测器与流模型；达到初步收敛后，冻结牵引力预测器，仅微调流模型。实验表明，此策略能有效提升 OOD 检测性能。但我们未观察到文献 [16] 所建议的“warm-up”策略带来额外提升。

超参数搜索：Adam优化器学习率：, , ]；当使用 UEMD² 与 UCE 单独训练时，entropy 权重：；当联合使用时，UCE权重固定，仅搜索 UEMD² 权重：。对于每组超参数，我们用 5 个随机种子训练模型，并以验证集上的 EMD² 误差为指标选择最佳模型。实证表明，相比使用 KL 散度选择模型，用验证集的 EMD² 误差选择模型能提升整体表现。为公平起见，图表结果统一基于 UCE 损失 + 验证集 KL 散度选出的模型。

图 10. 以 EMD² 和 KL 散度衡量的预测误差（越低越好）以及以 AUC-ROC 和 AUC-PR 衡量的 OOD 检测准确率（越高越好）。每个损失函数的图例后面的括号中是选择超参数的标准。结果显示平均值和标准差。总体而言，当给定更多训练样本时，所提出的 UEMD² 与 UCE 加权和可获得最佳预测准确率，并稳步提高 OOD 检测性能。由于训练和测试环境之间的分布偏移，过多的训练数据会导致其他损失设计的预测准确率下降。此外，与基于 EMD² 的损失相比，UCE 在捕捉离散牵引值之间的跨箱关系方面更差，导致预测准确率更差和 OOD 检测性能不稳定。

C. 预测精度与 OOD 检测性能

我们对不同的损失函数变体（公式 19）在以下两个方面进行了评估：预测精度（prediction accuracy）：使用 EMD² 与 KL 散度，即将预测分布与真实 GT 分布进行比较；OOD 检测性能：计算潜空间密度的 AUC-ROC 与 AUC-PR，相对于 OOD mask。AUC-ROC 与 AUC-PR 是二分类标准指标，数值越接近 1 代表分类越好，0.5 表示与随机分类等价。为对比上限性能，我们纳入了一组模型，在训练时直接使用 GT traction 分布（不采样）进行 UCE 训练。评估报告在图 10 中展示，包含 所有地图单元格、测试环境与随机种子的平均性能与标准差。

实验主结论：使用我们提出的 UEMD² + UCE 加权组合损失 所训练的模型，在 EMD² 和 KL 两个指标上均取得了最佳预测精度；该加权组合也带来了更稳定的提升，在训练样本增多时，OOD 检测性能与预测精度持续改善；但当训练样本过多时，预测精度会下降（尤其在非组合型损失下）——我们推测其原因在于训练与测试分布发生偏移，验证集仍表现良好；UCE 局限：与 EMD² 类损失相比，UCE 无法建模牵引力分布中 bin 间的相关性；导致潜空间表征欠规整，进而引起 OOD 检测性能不稳定；即使训练时使用 GT 分布也不能完全弥补这一缺陷。

表 II UEMD² 与联合训练的消融研究

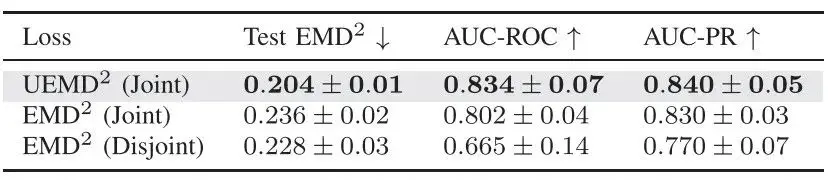
所示结果是基于多个随机种子计算所得的均值与标准差。最佳结果以粗体标出。

D. UEMD² 与联合训练的消融实验

虽然文献 [16] 已经证明：在使用 UCE 损失时引入不确定性感知与联合训练能够显著提升性能，但我们为完整性起见，也对 UEMD² 损失进行了类似的消融实验，相关结果见表 II。为了简化实验，我们将样本数倍增因子设为 10（即牵引力采样量扩大 10 倍）。但在其他倍增设置下也可以得出类似结论。实验结果表明：只有同时使用联合训练与不确定性建模（如 UEMD²），才能在 EMD² 精度与 OOD 检测方面显著改善。尽管上述策略已经带来改进，但图 10 的结果进一步表明：想要获得更一致、稳定提升的预测精度与 OOD 检测性能；仍需联合使用 UEMD² 与 UCE 两种损失函数。

Ⅵ 风险感知规划器的评估

在模拟的 2D 语义环境中，地形牵引力具有较高的 Aleatoric 不确定性。实验表明，我们提出的 CVaR-Dyn 方法相较于现有方法（如 [11], [21]）在假设名义牵引力或期望牵引力的前提下具有更优性能，同时在效果上也能与 CVaR-Cost 方法 [22] 竞争。为简化评估，我们构建了一个网格世界环境，其中 dirt 与 vegetation 单元格具有已知牵引力分布（见 图 11）。植被单元格随机生成，其密度在地图中心逐渐增加。由于植被对应的是一个双峰牵引力分布，机器人容易陷入“失去动力”的陷阱。任务目标：机器人需避开零牵引力区域、避障，并成功到达目标点；若机器人无法移动或陷入局部最优轨迹（如原地打转），视为失败。

图 11. 模拟环境，机器人必须在有界区域内尽快从起点移动到目标。为简单起见，线性和角牵引力参数具有相同的分布。植被地形斑块在植被区域的中心随机采样。

A. 规划器实现细节

我们使用 MPPI（Model Predictive Path Integral, [18]）进行控制；时域：100 步，步长 0.1s；控制信号：线速度 3 m/s，角速度 π rad/s，带有噪声（2 m/s, 2 rad/s）；rollout 数量为 1024；对牵引力分布使用 20-bin PMF 进行近似；所有模拟运行在 GPU 上（i9 + RTX 3070），其中 CVaR-Cost 是最昂贵的计算方式，但能以 15 Hz 的频率重新规划（200×200 地图尺寸）；未进行牵引力采样的规划器可运行至 50+ Hz。

B. 导航性能对比

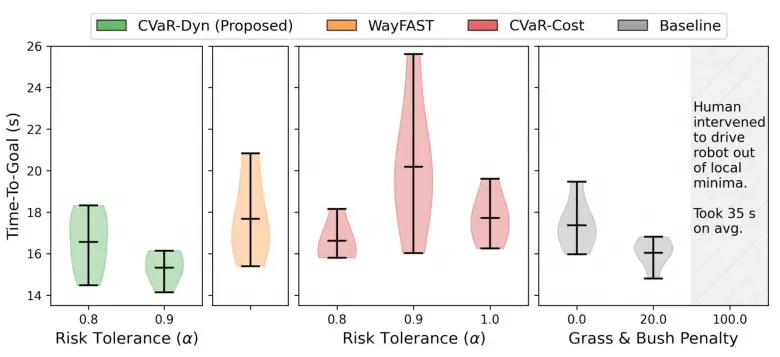
我们对以下方法进行了对比：CVaR-Dyn（本文方法）CVaR-Cost [22]WayFAST [21]：使用视觉感知的期望牵引力[11] 方法：使用名义牵引力 + CVaR 时间加权我们在所有方法中统一调整风险参数 ，WayFAST 固定为 。每个语义地图采样 5 组牵引力，重复 40 次实验。图12 总结结果：若 设得较小，CVaR-Dyn 在成功率与到达时间上均优于或接近 CVaR-Cost；图13 展示折中关系：不同方法在成功率与到达时间之间的取舍。

核心发现与对比分析：所有方法均可通过调参提升性能（除 WayFAST）；为 vegetation 设置高惩罚项（名义牵引力方法）可最大化成功率；CVaR-Dyn 与 CVaR-Cost 在某些任务中可实现更快完成任务但略低成功率，适用于高风险、时间敏感任务；当  进一步降低时，CVaR-Dyn 更容易陷入局部最优，因为使用最坏牵引力后 rollout 过短；CVaR-Cost 的性能下降也明显，原因是 CVaR 目标本身估计更难；CVaR-Cost 解算时间约为 60 ms，其他方法约为 5 ms；整体而言，没有方法完全优于其他，需依据场景做决策。

实践建议与结论：在有领域知识时，可将 OOD 植被设为惩罚区域，配合 CVaR 规划器提升性能（见 Section VIII）；虽然仿真中 CVaR-Dyn 与 CVaR-Cost 表现接近，但在实际硬件测试中（见 Section IX），CVaR-Dyn 展现出最优综合性能。

图 12. 提出的 CVaR-Dyn、CVaR-Cost [22] 和 WayFAST [21] 分别使用预期牵引力和假设标称牵引力 [11]（即无滑移）的方法所实现的成功率和目标时间。需要注意的是，如果机器人达到目标，则任务成功。我们展示了目标时间的分布及其平均值。总体而言，当风险承受能力足够低（例如）时，CVaR-Dyn 的成功率和目标时间与 CVaR-Cost 规划器相似或更高，并且优于 WayFAST 和假设标称牵引力的方法。

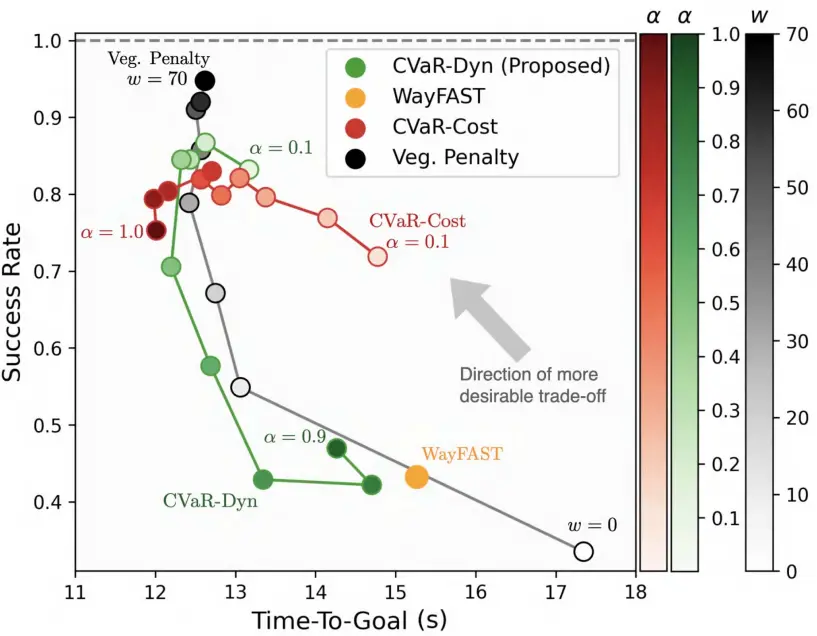
图 13. 在最具挑战性的 70% 植被覆盖场景中，成功率与目标达成时间之间的权衡，如果达到目标，则视为成功。CVaR-Dyn 和 CVaR-Cost 均比 WayFAST 实现了更好的权衡，位于图的左上角。当成功率低于 0.9 时，CVaR-Dyn 和 CVaR-Cost 比假设名义牵引力，同时对进入植被地形的状态施加辅助惩罚  的方法实现了更好的权衡。然而，随着  的减小，CVaR-Dyn 和 CVaR-Cost 的成功率会趋于平稳并最终下降，因为规划器变得更加规避风险，并且容易受到局部最小值的影响。

Ⅶ 优化 EMD² 提升导航性能

为支持本文的关键论点——EMD² 是比 KL 散度更优的度量指标，更适合评估可通行性模型中牵引力分布的学习质量，我们对采用不同损失函数训练的模型进行了导航性能评估，所涉及的模型已在第 V 节中介绍。这些模型被部署到与 图9 所示相同的测试环境中：每张地图为 30×30 米，起点与终点设在对角线两端；为简洁起见，本文只展示 CVaR-Dyn 规划器（α=0.4）下的结果，使用与第 VI-A 节一致的 MPPI 设置；但在不同 α值设定下也可观察到相似趋势。与第 V 节的 benchmark 保持一致：每种损失函数均使用 5 个随机种子 + 5 个不同训练数据量的设置；对 20 张测试地图中的每一张，采样 5 个牵引力图并运行 3 次任务；平均结果绘制于图14，因全部成功，故省略成功率。

图 14. 在图 9 所示的测试环境中，使用不同损失设计训练的学习牵引模型的导航性能。结果显示了所有测试环境、采样牵引图和随机种子的平均值和标准差。需要注意的是，所提出的混合损失的导航性能接近于在测试环境中使用 GT 牵引模型的最佳导航性能，以及在训练环境中使用 GT 牵引分布训练的最先进的 UCE 损失的最佳导航性能。

关键发现：在训练数据稀缺的情况下，尽管 UEMD² 的 KL 误差略高于 UCE（如 图10 所示），但 UEMD² 在时间效率上优于 UCE；这验证了我们的直觉：EMD² 能更好捕捉牵引力分布的 cross-bin 结构，在小数据 regime 中提供更好的泛化能力；数据量增加后，我们提出的 UEMD² + UCE 加权混合损失在导航性能上全面超越其他方法。然而，如第 V-C 节所述，当训练数据过多时，会引发训练与测试分布之间的偏移，导致牵引力预测性能下降 → 导航性能下降（见 图14）。但混合损失方法对此不敏感，能更好保持导航性能；此外，混合损失在低数据设置下接近使用 GT traction + UCE 损失的最优性能上限；这说明：仅使用训练环境中圆形路径采样到的有限数据，混合损失方法就能实现良好的泛化能力。图中还提供了一个下界（lower bound），即基于测试环境中 GT traction 模型所计算的最短到达时间。

Ⅷ 避开ODD地形的优势

我们展示了基于密度的置信度分数（公式 (9)）在检测高 epistemic 不确定性地形方面的效果，以及在导航过程中避开 OOD 区域的实际收益。实验设置：使用 Clearpath Husky 机器人，在两个不同的森林区域采集数据；第一个区域用于训练（见 图5）；第二个区域为测试场景（语义地图见 图15）；使用语义八叉树 [50] 构建环境模型，将 LiDAR 与语义分割 RGB 图融合，语义分割基于 RUGD 数据集的 24 类（见 [52]）；测试环境中的地面真实牵引力由另一套神经网络估计，用作 proxy-GT。我们使用 CVaR-Dyn（α=0.2）来适应牵引力预测的高噪声，主要研究在具有新颖语义地形特征的区域中的导航表现。实验设计：在测试地图中设定两个具挑战性的 start-goal 点对；每组点对在不同置信度阈值下重复 10 次；对比两种方式避开 OOD 地形：将 OOD 区域设为“0 牵引力”；赋予 OOD 区域高额代价惩罚。若成功抵达目标即视为任务成功。

图 15. （左）在测试环境中，模拟机器人必须达到两个选定的目标，以强调使用不可靠网络预测的危险。（右）基于潜在密度的置信度得分 (9) 表示预测牵引力分布的认知不确定性程度，其中未知地形和已知地形的负值得分以黑色表示。请注意，由于存在未知单元，顶部的棕色语义区域（覆盖物）的置信度低于零，而左侧的棕色语义区域则包含较少的未知单元。 

实验结果如图 16 所示：随着置信阈值 的提高，成功率最多可提升至 30%；这是因为机器人有效地避开了牵引力预测不可靠区域。此外，当为 OOD 地形使用“软惩罚”策略（而非直接禁止）时：能够在保证类似成功率的前提下，显著提升任务完成效率（time-to-goal）；原因是惩罚机制引导规划器更容易找到避开 OOD 区域的路径。因此，当可利用场景知识时，将辅助代价项与 CVaR-Dyn 方法联合使用：不仅能提升成功率；还可实现更快、更稳定的导航；是在实际部署中非常有价值的策略。

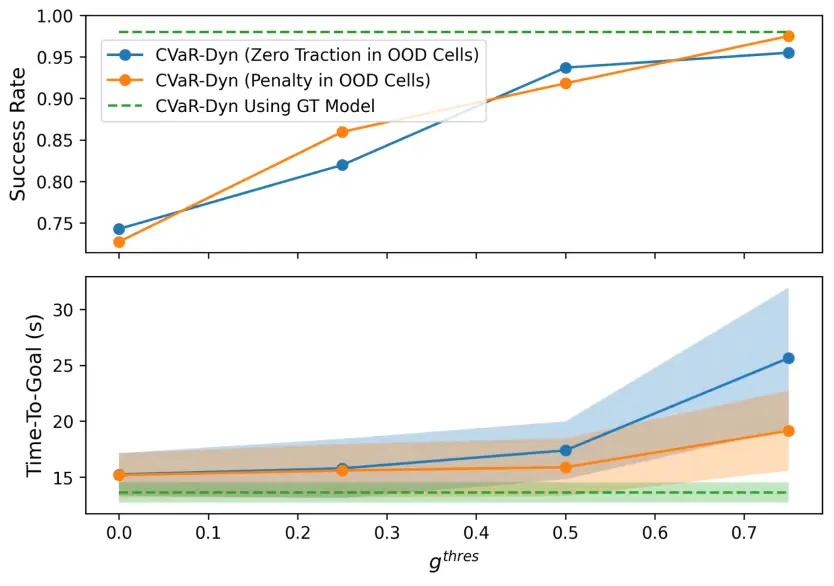
图 16. 通过避开 OOD 地形，导航成功率有所提升。注意，阴影区域表示标准差。OOD 地形的处理方式为：分配零牵引力（蓝色）或施加惩罚（橙色）。图中包含了使用 GT 牵引力的规划器的性能，以展示最佳性能。总体而言，更高的   值提高了成功率，但代价是缩短了目标时间。然而，针对 OOD 地形的辅助惩罚，使规划器更容易找到实现目标的解决方案。值得注意的是，当 时，平均成功率趋近于 1，这表明学习到的牵引力模型在测试环境中能够很好地推广到具有高置信度值（低认知不确定性）的地形。

实践结论：因此，当可利用场景知识时，将辅助代价项与CVaR-Dyn 方法联合使用：不仅能提升成功率；还可实现更快、更稳定的导航；是在实际部署中非常有价值的策略。

Ⅸ 硬件实验

为了验证 EVORA 的有效性与可行性（即本文提出的不确定性感知可通行性学习与风险感知路径规划的整体框架）在实际中的应用效果，我们设计了两个实验场景：一个使用遥控车的室内赛道任务，模拟带有假植被的环境（见 Section IX-A）；另一个使用四足机器人的更具挑战性的室外导航场景（见 Section IX-B）。在两个场景中，机器人都使用车载传感器在测试时在线构建环境地图，这引入了来自运动模糊、光照变化与不完整地图等问题带来的更大不确定性。虽然两个实验都表明，所提出的 CVaR-Dyn 路径规划器在导航性能上表现最佳，室外实验场景还进一步展示了避开 OOD 地形的优势。在实际中，由 MPPI 生成的控制信号通常非常嘈杂，因此我们在名义控制 [54] 的导数空间中进行规划，以生成平滑轨迹。

A. 使用遥控车的室内竞速实验

本节实验的目标是展示在控制环境中，所提出的规划器在缓解 aleatoric 不确定性所带来风险方面的性能优势。

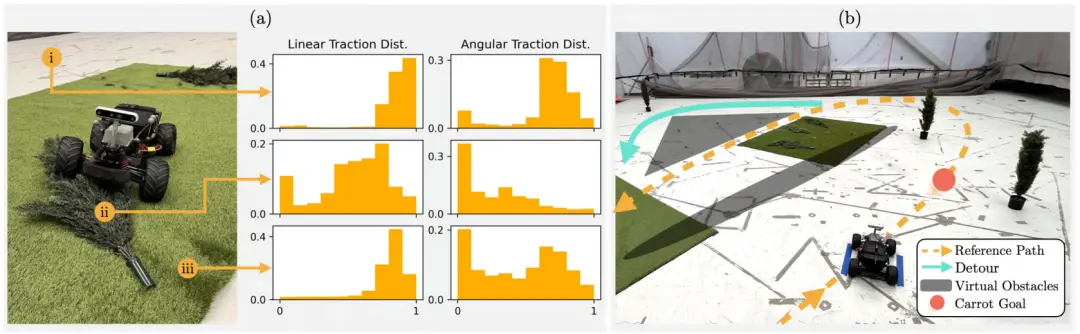
图 17. 用于室内赛车实验的训练和测试环境。(a) 训练环境由一块草坪和两棵倒下的树木组成，用于模拟灌木丛。学习到的线性和角度牵引力分布在选定区域可视化，包括 (i) 硬地板、(ii) 倒下的树木和 (iii) 草坪。需要注意的是，植被上牵引力分布的双峰性可能会导致机器人速度显著降低。(b) 测试环境包含两块草坪、三棵倒下的树木、三棵直立的树木和虚拟障碍物。机器人的任务是沿着参考路径跟随胡萝卜目标行驶两圈，同时在无植被的绕行路线和有植被的较短路径之间做出选择。(a) 训练环境中学习到的牵引力。(b) 测试环境。

1)实验设置：

如图17 所示，室内环境占地面积为 9.6 米 × 8 米，为了与 0.33 米 × 0.25 米的 RC 小车一致，场地内部设置了一条由人造草皮与假树组成的路径，以模拟户外的植被区域。小车上安装了 RealSense D455 深度摄像头、Intel Core i7 CPU 与 Nvidia RTX 2060 GPU。机器人在车载平台上执行牵引力预测、运动规划与高程图建图，建图分辨率为 0.1 米，但实际位姿与速度估计由 Vicon 完成。植被识别方式为：提取图像中绿色像素点，而不是使用单独的语义分割网络，以节省 GPU 资源。路径传播模型使用公式 (3) 所示的 bicycle 模型，牵引力由命令线速度、转向角与 Vicon 所提供的 GT 实际速度进行标定计算得出。

我们基于 10 分钟的驾驶数据对牵引力模型进行训练，使用的是所提出的联合损失函数 (19)，即加权组合的 UEMD² 和 UCE：两者的加权系数均设为 1；熵项加权系数为 1e-5（经验调优得出）；所学习得到的牵引力分布如图17(a) 所示，呈现多峰性（multimodality）。在部署时，机器人需在赛道上绕跑两圈，并根据下述两条路径进行决策：一条路径较短，但包含植被；另一条路径较长，但风险较低，如图17(b) 所示。我们设计了一个动态目标区沿着椭圆形参考轨迹运动，该目标点被称为“胡萝卜目标（carrot goal）”，它与机器人在参考路径上的投影点保持 75° 的固定偏移角。

在方法对比方面，我们考虑：CVaR-Cost；本文提出的 CVaR-Dyn；一个基线方法：假设使用名义牵引力，但对高度在 5 cm 到 15 cm 之间的低矮植被区域引入辅助惩罚项，因为这些区域可能导致驾驶困难。所有方法都通过辅助惩罚机制避开植被区域。所有规划器均执行：在 20 Hz 下进行规划；展望步长为 5 步；每次生成 1024 个 rollout；CVaR-Cost 由于计算成本更高，仅使用 400 个牵引力图样本；最大速度设为 1.5 m/s，最大转向角设为 30°。

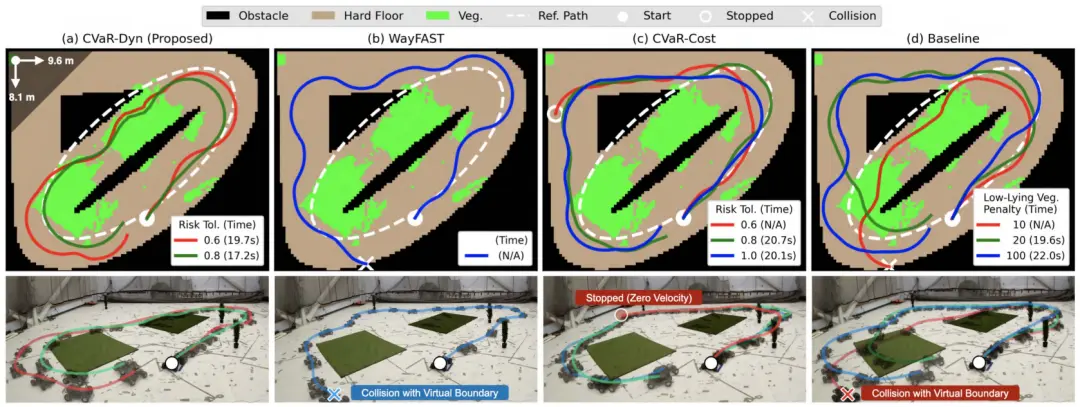
图 18. 室内实验的代表性试验，用于突出规划器的故障模式。上行显示自上而下的语义地图，下行显示延时照片。为了清晰起见，我们仅显示两圈中的第一圈。（a）随着  的减小，提出的 CVaR-Dyn 变得更加规避风险，并采取更大的转弯以进入捷径。（b）WayFAST（ 的 CVaR-Dyn）没有考虑转向不足的风险，因此它总是转弯太晚而无法走捷径。（c）CVaR-Cost 始终绕道行驶以避开植被地形。随着  的减小，规划器变得更加规避风险，有时会在障碍物附近停止。（d）当软惩罚较低时，基线更具风险承受能力并会选择捷径，但实际牵引力与标称牵引力存在显著差异，导致更多碰撞。随着软惩罚的增加，规划器变得更加保守并绕道而行，但使用标称牵引力进行规划会导致严重的转向不足，从而限制性能。

图 19. 室内实验 5 次试验的结果和任务时间。我们展示了任务时间的分布以及最大值、平均值和最小值。提出的 CVaR-Dyn 在  时实现了最佳目标时间，成功率为 100%。随着  的减小，CVaR-Dyn 和 CVaR-Cost 都会导致目标时间缩短。需要注意的是，当  时，CVaR-Cost 在许多情况下会在障碍物附近停止。相比之下，基线和 WayFAST 会导致更差的目标时间，并且发生碰撞的可能性更高。

2)Aleatoric 不确定性结果分析：

我们对比了各个规划器在缓解由于 aleatoric 不确定性引起的导航风险方面的能力，定性与定量结果见图18 和 图19。考察了三种风险容忍度 ；辅助惩罚项设定为 ；对于名义牵引力规划器，将所有进入植被区域的状态都视为“高风险”状态；WayFAST 方法单独呈现，作为 CVaR-Dyn（）的一种特例。我们对每组设置进行五次重复实验，每次包括两圈比赛。整体结果表明：CVaR-Dyn（）在平均成功率与最短时间到达方面均表现最佳。图18 中的定性可视化表明：基线方法与 WayFAST 在现实世界的牵引力噪声下容易偏离轨迹、转向发散；而 CVaR-Cost 与 CVaR-Dyn 能够通过生成平滑轨迹更好地应对该噪声；CVaR-Cost 更容易绕远路，并在障碍物附近容易陷入局部极小值。

B. 使用腿式机器人进行户外导航

与室内环境相比，户外实验中地形类型更加多样，感知中的不确定性也更大，这主要是由于光照变化和剧烈运动所引起的。除了评估规划器处理阿列阿不确定性（aleatoric uncertainty）的能力之外，户外测试还展示了通过避免 OOD 地形（分布外地形）来减缓认知不确定性（epistemic uncertainty）带来的风险的好处，同时也验证了我们方法在腿式机器人上的适用性。

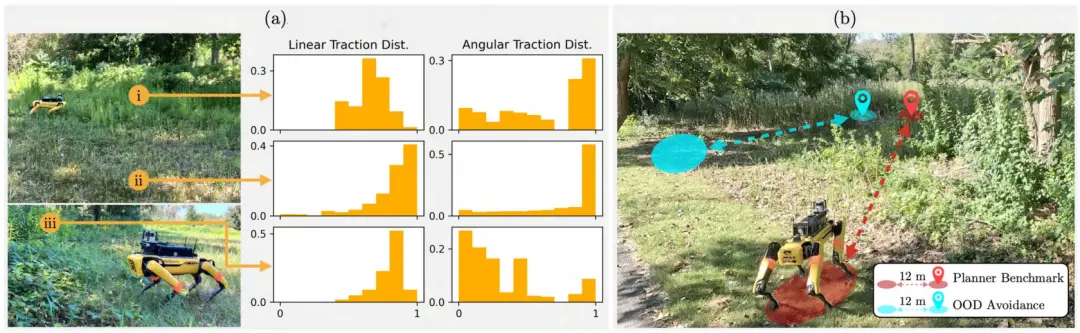
图 20. 腿式机器人的户外训练和测试环境。(a) 户外环境由不同高度和密度的植被地形组成。可视化了选定区域的预测线性和角度牵引力分布，这些区域包括 (i) 高草、(ii) 短草和 (iii) 茂密的灌木丛。与轮式机器人不同，腿式机器人在穿过植被时通常具有良好的线性牵引力，但由于转弯难度较大，角度牵引力可能表现出多模态性。(b) 使用两对起始-目标样本对规划器进行基准测试，并分析避开 OOD 地形的优势。(a) 在训练环境中学习到的牵引力。(b)测试环境。

1）实验设置

图20 展示了户外实验的整体设置概况。一台 Boston Dynamics 的 Spot 机器人被装备了 RealSense D455 深度相机、Ouster OS0 激光雷达，以及 Nvidia Jetson AGX Orin（该设备在功耗效率上优越，但计算能力较我们前面实验中使用的计算平台要低）。本实验采用了单轮车模型（unicycle model，参见公式 (2)），牵引力的数值是通过比较机器人的控制指令与其内置里程计输出的实际运动结果计算得出的。环境地图是通过构建语义八叉树（semantic octomap）得到的，八叉树以 0.2 m 的分辨率将激光雷达点云和基于 RUGD 数据集 [52] 提取的 24 类语义标签的 RGB 图像融合而成。牵引力模型基于 5 分钟的行走数据进行训练，使用的是我们提出的损失函数（19），其权重与室内实验中的设置相同。所学习到的牵引力分布在图20(a) 中可视化展示，用以突显其多模态特性。如图20(b) 所示，我们选择了两个起点-目标点对，以测试不同规划器在避开 OOD 地形方面的效果及其带来的好处。所有规划器都会通过附加代价机制避免进入海拔高于 1.4 m 的地形区域；而基线方法（baseline）还会对高度低于 1.4 m 的草地与灌木类语义类型地形附加软代价（soft cost）。尽管 1.4 m 的高度阈值远高于机器人的步高，但所选测试环境中并不包含短小且刚性的障碍物，这是为了分析各类规划器在应对高植被环境方面的能力。由于语义分类、牵引力预测与运动规划模块需共享 GPU 资源，规划器只能以 5 Hz 的频率进行规划，并能提前预测 8 秒路径，共执行 800 次控制采样。CVaR-Cost 方法由于计算限制仅允许使用 200 张牵引力地图采样。最大线速度和角速度分别为 1 m/s 与 90°/s。

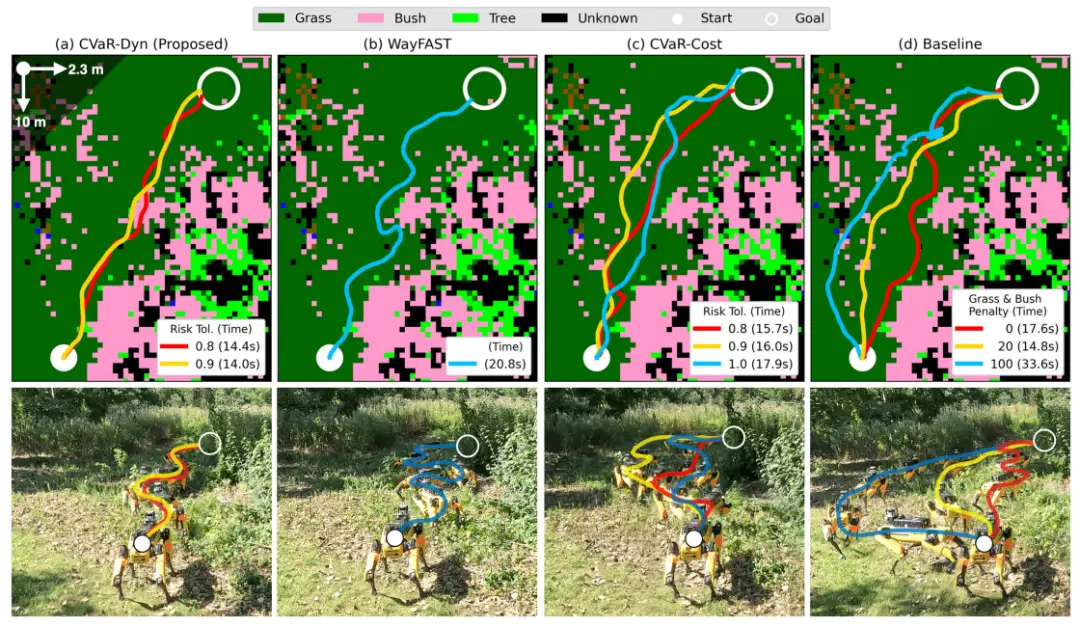
图 21. 户外实验的代表性试验。上行显示自上而下的语义地图，下行显示延时照片。（a）与其他方法相比，提出的 CVaR-Dyn（）能够很好地处理嘈杂的地形牵引力，并且产生的轨迹波动更小。（b）WayFAST（ 时的 CVaR-Dyn）依赖于预期牵引力，这无法很好地指示实际轨迹结果，导致航向不断修正。（c）与 CVaR-Dyn 相比，CVaR-Cost 更为保守，因为它远离灌木丛并实现了更长的目标时间。（d）基线假设标称牵引力，这会导致转向不足。随着软惩罚的增加，机器人越来越不愿意面对高高的草丛和灌木丛。由于大部分测试区域都被草丛或灌木丛覆盖，因此具有较大软惩罚的基线在后续试验中难以找到可行的计划来实现目标。

图 22. 局部规划器基准测试的目标时间分布，包含最大值、平均值和最小值。每个规划器总共完成三次往返，即六次试验。提出的  的 CVaR-Dyn 性能优于需要更多计算的 CVaR-Cost、使用预期牵引力进行规划的 WayFAST（ 的 CVaR-Dyn）以及使用标称牵引力进行规划并对草地和灌木丛施加软惩罚的基线。

2）阿列阿不确定性结果

图 21 和图 22 展示了在应对阿列阿不确定性风险方面，各类规划器的定性与定量比较结果。我们每个方法都重复执行三次往返路径（共六次试验）。整体而言，CVaR-Dyn 在 设置下取得了最佳的耗时与成功率表现，与第 IX-A 节中的室内实验结果一致。CVaR-Cost 的策略更保守，常常会远离草丛区域。相比之下，基线方法与 WayFAST 都受到真实牵引力噪声的影响，轨迹弯折严重。特别地，当对草地与灌木地形的软惩罚设置得过高时，基线方法容易陷入局部最小值（local minima），需要人工干预，导致任务耗时变长。

图 23. 规划器规避 OOD 地形的典型行为，其中语义自上向下地图和延时照片分别显示在顶部和底部。如果没有 OOD 规避功能，机器人容易因在线地图不完善和地形牵引噪声而陷入局部极小值，需要人工干预才能远程操作机器人到达可行目标规划区域。相比之下，为 OOD 地形分配辅助惩罚项，则使规划器更容易找到到达目标的轨迹。

图 24. 六次试验（三次往返）OOD 避让测试的目标时间分布，包括最大值、平均值和最小值。通过避开 OOD 地形，规划器不易受到局部极小值的影响，并通过避开训练期间未见过的特征地形，实现了更佳的目标时间。

3）认知不确定性结果

与前面的实验不同，OOD 地形规避实验的目标是展示在面临认知不确定性风险时采取缓解措施的效果。因此，我们仅使用 CVaR-Dyn（）进行评估，但如果将底层的局部规划器替换为 CVaR-Cost 或其他用于缓解阿列阿不确定性的方法，也能得出相似结论。我们总共执行三次往返路径实验。图 23 和图 24 展示了 OOD 规避实验的定性与定量结果。我们将某一地形视为 OOD，当其牵引力预测器的 latent 特征密度归一化后低于 0（即低于训练数据中所有特征密度的 0 百分位）。更保守的阈值可以基于经验调节获得。与图20 中的训练环境相比，图23 中的测试环境包含大量训练集中未见的高植被区域。因此，这些高植被区域会产生较高的认知不确定性，对应的地形将被标记为 OOD。如果不避开 OOD 地形，机器人容易陷入局部极小点，需要人为干预才能将其移至可行轨迹区域以继续前往目标点。相比之下，避开 OOD 地形的规划器能在不依赖人工干预的情况下获得更短的时间开销。

C. 硬件实验总结

此外，估计认知不确定性（epistemic uncertainty）的能力使我们能够识别并规避具有不可靠牵引预测的 OOD 地形，从而提升导航成功率并减少人工干预。

Ⅹ 局限性与未来工作

从建模角度来看，本工作聚焦于二维机器人模型，但面对更具挑战性的地形时，六自由度（6-DoF）模型是必要的 [36], [55], [56]。此外，我们使用 语义八叉树（semantic octomap） [50] 来建模环境，但也可以采用计算成本更低的替代方法 [10], [57]。此外，我们的系统依赖于语义分割模块的精度，因此当测试环境与训练环境差异较大（例如光照或季节变化导致）时，所提出的管线可能会失效。因此，感知模块中不确定性带来的风险需要单独研究 [41]。从数据采集角度来看，本研究依赖于用于训练的真实牵引分布，而这种分布对于高维特征（如 RGB 图像）可能难以获取。虽然我们提出的损失函数可用于直接训练即时牵引测量，但使用 EMD² 损失 所带来的性能提升仍需进一步评估。此外，也可以使用基于不确定性的主动采集方法 [37], [58] 来收集更具信息量的训练样本。从规划角度来看，本研究提出了使用牵引 CVaR 来模拟状态轨迹的方法，但仍需要进一步研究将该思想推广至更多系统参数与性能指标的通用性。此外，我们的规划器能够在新环境中避免 OOD 地形，但只能在有人工干预时进行在线适应 [12]。最后，所提出的方法也可以与利用远场信息的全局规划器 [59] 结合使用。

XI 结论

本工作提出了 EVORA，这是一个统一的框架，用于基于证据深度学习的不确定性感知可通行性学习，以及基于 CVaR 的风险感知规划。EVORA 通过经验分布（代表 aleatoric 不确定性）建模地形牵引力的不确定性，并基于牵引预测器潜在特征的密度（代表 epistemic 不确定性）识别 OOD 地形。通过利用我们提出的不确定性感知的平方 EMD 损失函数，我们提升了神经网络的预测准确率、OOD 检测性能以及下游导航性能。为应对 aleatoric 不确定性，所提出的风险感知规划器基于牵引分布的左尾 CVaR 来模拟状态轨迹。为应对 epistemic 不确定性，我们提出为那些潜在特征密度较低的地形分配辅助代价，从而提升导航成功率。整个系统通过大量仿真实验和硬件实验进行了分析，展示了其在不同地面机器人平台上的导航性能提升。

附录 A：UCE 损失与 Dirichlet 熵（参考 [16]）

给定  和目标 ，

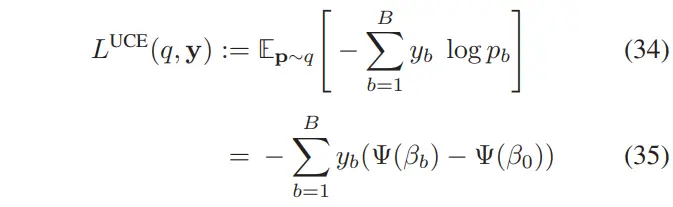
其中 是 digamma 函数，≔β 是整体证据。此外， 的熵为：

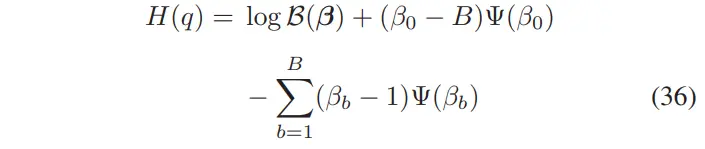
其中  表示 beta 函数。

附录 B：定理 1 的证明

我们从 UEMD²的定义出发（参考式 (17)），并通过使期望中 变得隐式来简化记号。记  为目标 PMF，为累积求和算子，记 为累积求和向量的第  项。

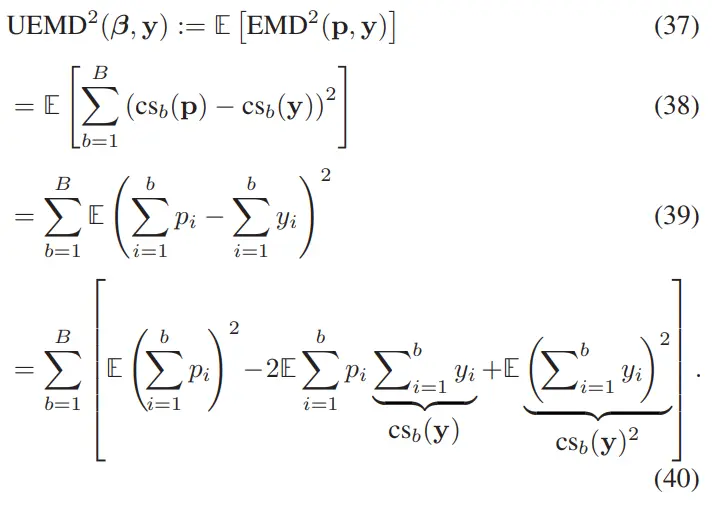
将恒定项 单独分出后，整理剩余项，并将期望移入求和内部，得到：

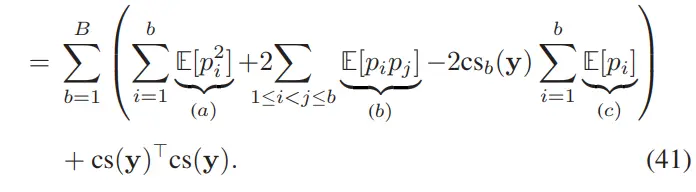
公式 (42)–(47) 给出了对 Dirichlet 分布的标准性质（均值、方差和协方差）的封闭形式：

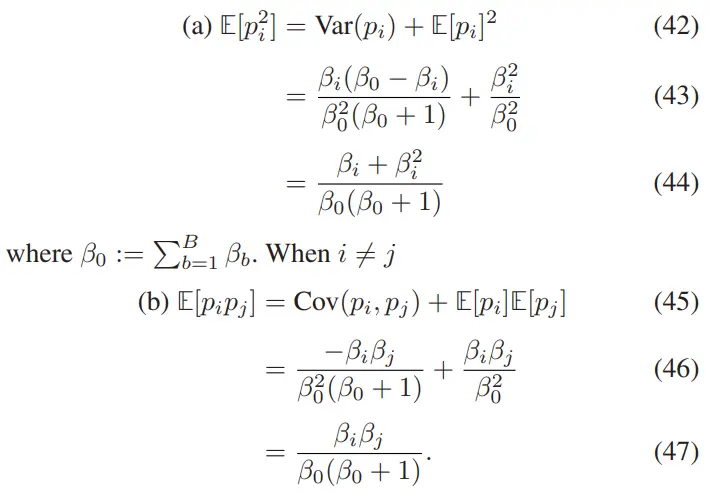
最终带入公式 (41)，得：

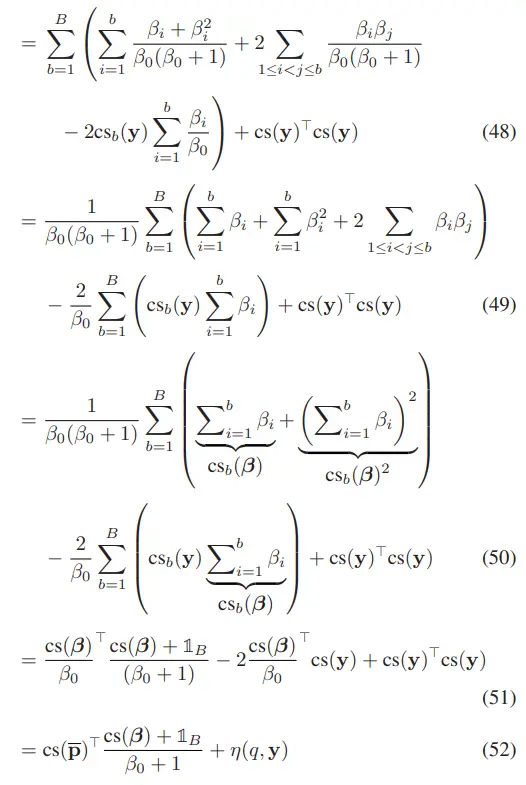
其中≔，见公式 (16)。

参考文献