分布式驱动车辆的多轴转向电子差速模型
为了避免分布式驱动车辆在转向过程中的轮胎异常磨损、防止不稳定驱动、实现车辆的平顺转向,同时,改善车辆操控性和安全性,一般要求所有车轮在转向过程中都作纯滚动。分布式驱动车辆在转向时需要做电子差速控制,如若考虑多轴转向的分布式驱动车辆,则主动转向系统与电子差速系统的协调控制就显得尤为重要。因此,本文针对四轮转向和六轮转向分布式驱动车辆的转向特性和电子差速问题进行研究。
01、四轮转向差速设计1.1
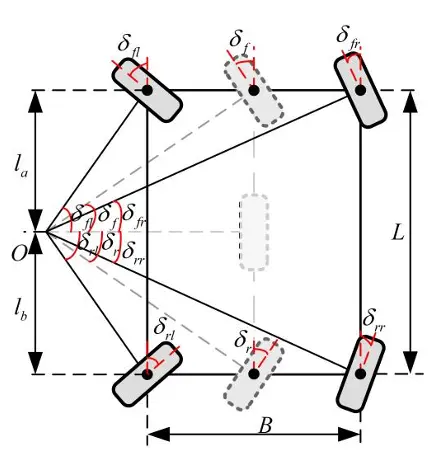
阿克曼四轮转向角度计算,对四轮转向车辆的运动学模型进行分析,以低速左转为例,此时后轮角度与前轮角度相反,如下图所示。
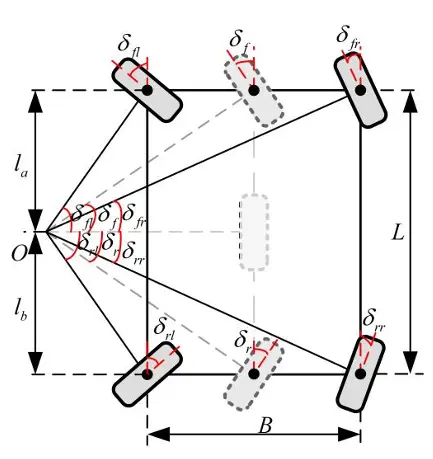
图1 四轮转向车辆运动学模型
根据车辆转向过程中的几何关系得到:
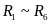
由上式可得:
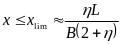
由图可以分析出左前轮的角度:
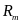
将R代入可求得左前轮转角并且可以表示为:
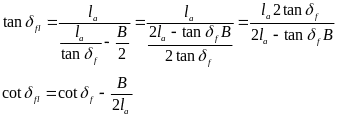
将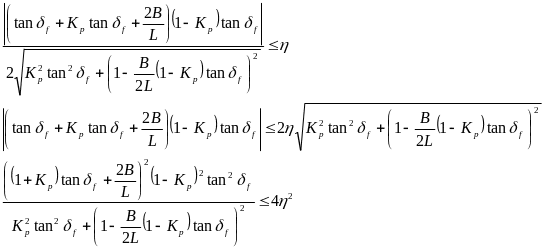 代入上式则左前轮角度可表示为:
代入上式则左前轮角度可表示为:
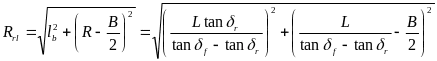
同理可以计算得到每个车轮的转角为:
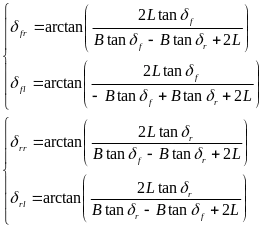
1.2 四轮转向差速设计
接下来,根据四个车轮的转向角度求每个车轮的转向半径:左前轮转向半径计算:
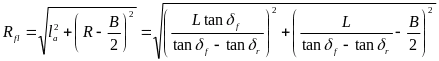
右前轮转向半径计算:
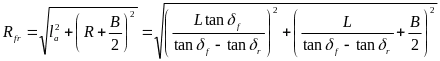
左后轮转向半径计算:
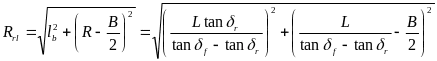
右后轮转向半径计算:
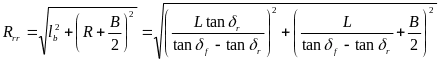
由转向瞬心定理可得:
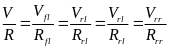
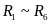
即,左前轮转速计算:
右前轮转速计算:
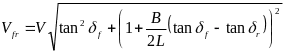
左后轮转速计算:
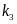
右后轮转速计算:
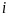
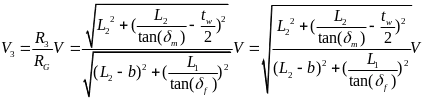
其中,Kp为前后轮的角传动比系数。根据车辆线性二自由度四轮转向模型的稳态转向特性可得:
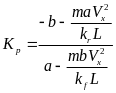
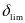 ,则当车速低于临界车速时-1<Kp<0,反之,当车速高于临界车速时0<Kp<1,则
,则当车速低于临界车速时-1<Kp<0,反之,当车速高于临界车速时0<Kp<1,则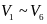 ,因此可得最大轮速为Vfr,最小轮速为Vrl,其最大轮速差为
,因此可得最大轮速为Vfr,最小轮速为Vrl,其最大轮速差为
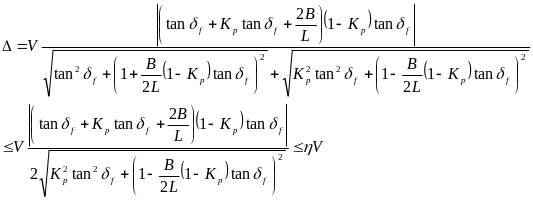
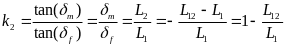 ,并采用
,并采用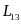 近似计算,则
近似计算,则
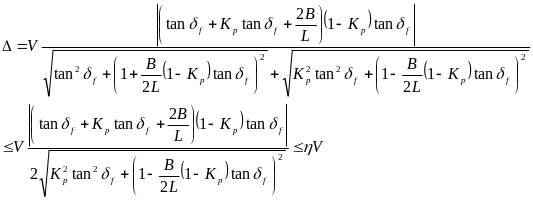
其中,η表示偏差的百分比,即,当最大轮速与最小轮速之差不大于车速的η倍时,则不需要进行主动的电子差速控制。因此,可得
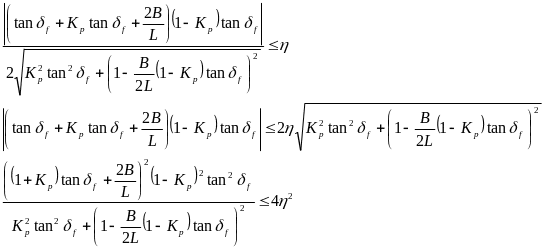
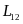 ,则
,则
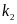
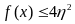 时则不需要进行电子差速,进而转化为求f(x)的极大值问题,只要保证最大的轮速偏差满足约束条件即可不做差速处理。经过计算可以发现,
时则不需要进行电子差速,进而转化为求f(x)的极大值问题,只要保证最大的轮速偏差满足约束条件即可不做差速处理。经过计算可以发现,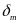 ,即非线性函数f(x)对x单调递增,因此,当
,即非线性函数f(x)对x单调递增,因此,当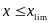 时即可保证
时即可保证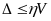 ,其中xlim满足
,其中xlim满足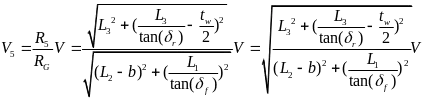 ,而当
,而当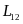 时必须进行电子差速。另一方面,f(x)也会受角传动比系数Kp的影响,经过求偏导数发现
时必须进行电子差速。另一方面,f(x)也会受角传动比系数Kp的影响,经过求偏导数发现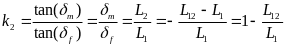 ,而-1<Kp<1,则当Kp=-1时,f(x)取最大值为
,而-1<Kp<1,则当Kp=-1时,f(x)取最大值为
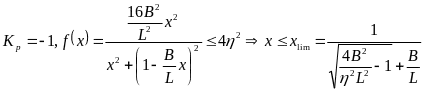
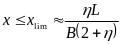 。在不同车速下可要求不同的速度偏差,即可确定临界的前轮转角
。在不同车速下可要求不同的速度偏差,即可确定临界的前轮转角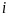 需电子差速的临界前轮转角,当前轮转角较小时则不需要做差速处理。针对某一特殊车型,取L=2B为例时,计算的临界前轮转角具体如下表所示。
需电子差速的临界前轮转角,当前轮转角较小时则不需要做差速处理。针对某一特殊车型,取L=2B为例时,计算的临界前轮转角具体如下表所示。
|
车速(m/s) |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
|
η |
0.05 |
0.04 |
0.035 |
0.03 |
0.025 |
0.02 |
0.015 |
0.01 |
0.01 |
|
(deg) |
2.795 |
2.247 |
1.971 |
1.694 |
1.415 |
1.135 |
0.853 |
0.57 |
0.57 |

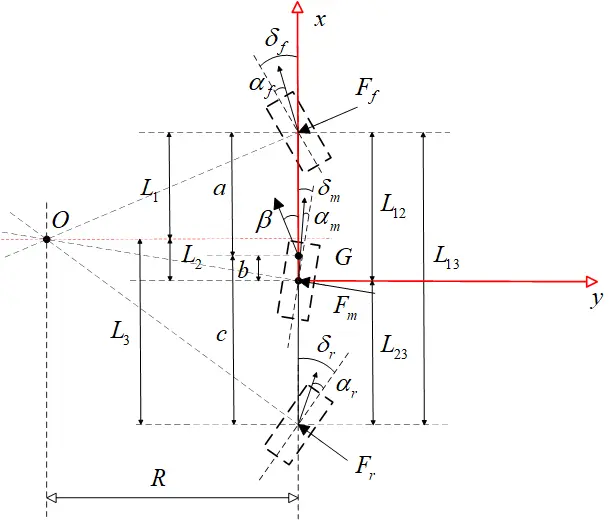
图2 六轮转向二自由度模型
使用如下车辆二自由度模型: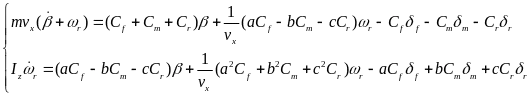 (1)对于三轴车辆,在假设第一轴转角已知的情况下,基于阿克曼转向几何关系,第二、三轴转角应满足以下关系:
(1)对于三轴车辆,在假设第一轴转角已知的情况下,基于阿克曼转向几何关系,第二、三轴转角应满足以下关系:
 (2)
(2)
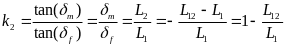 (3)
(3)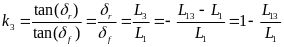 (4)
(4)
式中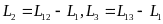 表示转向中心到第
表示转向中心到第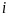 轴到的距离;
轴到的距离;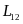 表示第二轴到第一轴的距离;
表示第二轴到第一轴的距离;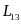 表示第三轴到第一轴的距离。
表示第三轴到第一轴的距离。
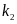 、
、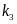 ,首先得到转向中心
,首先得到转向中心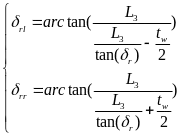 到前轴距离
到前轴距离 的表达式,令车辆的质心侧偏角
的表达式,令车辆的质心侧偏角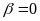 ,质心侧偏角速度
,质心侧偏角速度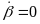 ,车辆在稳态转向时横摆角加速度满足
,车辆在稳态转向时横摆角加速度满足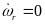 。由多轴车辆在转向时处在稳定状态下可得如下条件:
。由多轴车辆在转向时处在稳定状态下可得如下条件:
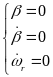 (5)
(5)
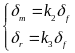 (6)
(6)
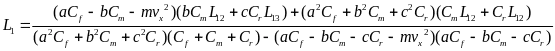
(7)
在各转角比例系数确定的情况下,每个前轮转角都对应一个转弯半径,由图1中几何关系可得知转弯半径与前轮转角有如下关系: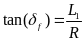 (8)
(8)
则前轮转角可以用转弯半径表示为:
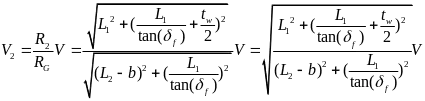 (9)
(9)
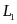 后,代入角传动比系数即可解得
后,代入角传动比系数即可解得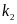 、
、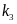 ,进一步的,根据式(6)求出
,进一步的,根据式(6)求出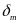 和
和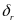 。根据阿克曼转向几何换算每个车轮的转角,关系如下:
。根据阿克曼转向几何换算每个车轮的转角,关系如下:
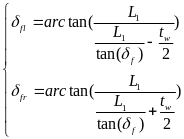 (10)
(10)
 (11)
(11)
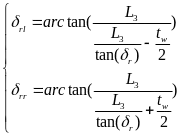 (12)
(12)
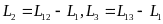 。根据低速转向时的电子差速模型,建立如下的车辆运动学模型:
。根据低速转向时的电子差速模型,建立如下的车辆运动学模型: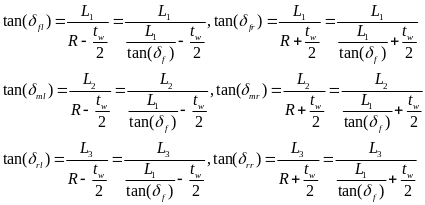
图3 六轮车辆转向运动学模型
其中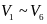 表示各个车轮的纵向速度,
表示各个车轮的纵向速度,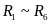 表示各个车轮绕转向中心,
表示各个车轮绕转向中心,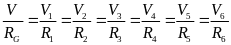 为运动半径,
为运动半径,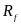 为前轴转动半径,
为前轴转动半径,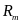 为中轴转动半径,
为中轴转动半径,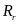 为后轴转动半径,
为后轴转动半径,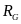 是质心绕转向中心的运动半径,
是质心绕转向中心的运动半径,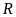 是转向中心到车轴中心线的垂直距离。
是转向中心到车轴中心线的垂直距离。
由几何结构可以得到以下关系式:
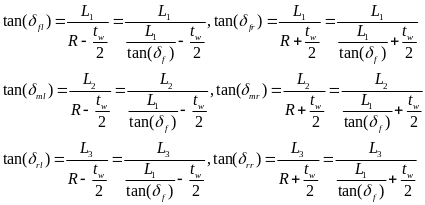
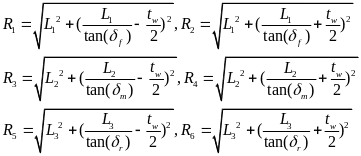
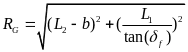
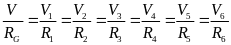
则当车辆左转时各个车轮纵向速度为:
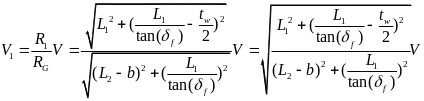
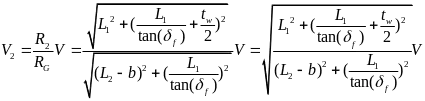
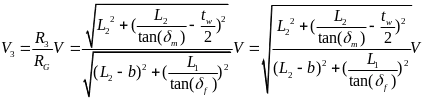
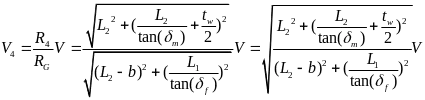
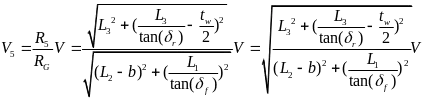
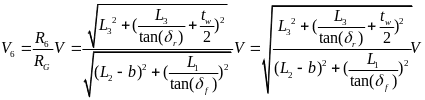
 广告
广告 最新资讯
-
联合国法规R76对轻便摩托车前照灯远近光性
2026-03-10 12:15
-
联合国法规R75对摩托车与轻便摩托车气压轮
2026-03-10 12:14
-
联合国法规R74对L1类车辆灯光与光信号装置
2026-03-10 12:14
-
联合国法规R73对货车侧面防护装置的工程化
2026-03-09 12:14
-
联合国法规R72对HS1卤素灯摩托车前照灯的工
2026-03-09 12:13





 广告
广告





























































