阶背式MIRA模型尾流双稳态行为的实验研究

本文报道了1/12阶背式MIRA模型在雷诺数Re=6.9e+5下的尾流场实验研究，聚焦于背部与行李箱盖的流动非对称性。在背部和行李箱盖设置了40个测压点来获得其表面压力分布，用2维PIV技术研究了尾流结构。对阶背结构上方瞬时压力信号进行分析，发现压力在展向上表现出双稳态现象，并在两个倾向值之间切换，而在垂直方向上没有这种现象。在z/H = 0.8平面上的瞬时速度场可分为三种模式，分别是两种双稳态和一种转换状态，非称状态的顺序是随机的。为了深入了解双稳态状态，对压力数据和基于PIV图片的获得的非定常尾流进行了条件平均，提取了这三种状态，发现两种双稳态现象统计对称。但在z/H = 0.44的平面上，并不存在双稳态现象。

介绍

汽车研究人员往往通过优化几何结构或控制策略来抑制尾流带来的不利影响，以实现节约能源的目的。与方背式车和快背式汽车相比，阶背式车的尾流结构更为复杂。背部后端的流动结构具有准二维及三维分离、回流流动、高湍流度等特点。Carr记录了不同顶盖长度、高度和背部倾斜角度组合下的表面流场模式，观察到剪切层从车顶后缘分离并重新附着在顶盖上。在背部后还发现了一个横向涡旋。Nouzawa等人研究发现，阶背的尾流模式基本由拱形涡和拖曳涡组成。阶背模型会增加阻力是因为顶端分离流降低了拱形涡内的压力，产生了强弯曲气流，弯曲气流产生了强的下洗气流，增加了尾涡的循环。然后Nouzawa等人进行了与Carr类似的研究，发现剪切层在一定条件下重新附着在行李箱盖上，同时也研究了背部后拱形涡增阻的非定常特性。Gilhome等人的研究发现了背部与行李箱盖相交区域存在回流泡，随后在顶盖上再附着，这是一个不稳定特征。Jenkins总结得到在顶板尾缘的流动分离是由两个顶盖涡主导的，这两个涡反向旋转，与后柱涡旋转方向相反，在背部后形成并向顶盖中心延伸。然而该研究并没有对流动结构进行完整的描述。Lawson等人在比例模型后观察到了流动的不对称，流动可视化的初步结果表明，起源于背部区域的流动不对称现象对雷诺数非常敏感，然而，PIV数据和流动静压数据结果表明，从背部到行李箱盖区域的不稳定程度对雷诺数几乎不敏感。因此，这种不对称是双稳态行为还是对雷诺数敏感目前不得而知。Gaylard等人汇总了许多案例，包括真实车辆和模型，观察到了阶背式车轮尾流不对称，根据这些情况并基于实验得出结论：这种不对称对自由流速度的变化不敏感。Gaylard等人]强调，需要进一步的工作来理解不同阶背几何的影响。此外，还不清楚不对称车轮的升、阻力性能有什么影响。Okada等人研究发现，非定常气动力是由行李箱盖上方独特的涡结构引起的，会导致车辆行进稳定性能的不同。Sims-Williams等人研究了阶背几何形状、气动阻力、流动不对称及非定常尾流结构之间的联系，发现不对称源于背部和行李箱盖区域，并随着阶背深度的增加而逐明显。Wood对不同背部角度下阶背模型的流场形式型进行了研究，得到35°背部下的高阻流场结构和低阻流场结构，并且发现40°背部角度下的阶背尾流结构与其他背部角度下的有很大不同。

其他轴对称体上也存在非对称现象，Mair等人发现在某种轴对称钝体后面很难得到轴对称分布的压力分布。Fabreet等人研究了球和平圆盘尾流的分岔和对称破裂。Herry 等人研究了零度滑移时三维双后向台阶下游的流动双稳态特性。Grandemange等人报道了一个三维钝体后部层流三维尾流的对称破裂的实验观察，发现这种破裂在大雷诺数下是持久的，双稳态湍流流尾流的产生与这一现象相关。随后，Grandemange等人对三维钝体后的双稳态行为进行了全面的研究。Grandemange等人进一步发现湍流尾流经过不同纵横比的平行六面体时具有双稳态特性。Volpe等人研究了全尺寸方背Ahmed模型非定常自然尾流中的双稳定性。Pavia et al.研究了Windsor模型双稳态尾流中不同动力学模式之间的随机关系（casual relationship），并提出了一个相平均低阶模型来详尽的描述双稳态之间转换的机理。综上所述，阶背型汽车的流动非对称现象早已被发现，似乎与方背式Ahmed模型后部的双稳态现象相类似。然而，我们还不理解这种类型的尾流运动情况以及非定常尾流与背压之间的联系。本研究关注阶背式MIRA模型的非定常尾流，和背部和行李箱盖上方上的双稳态现象。使用压力传感器探测瞬态背压，使用粒子图像测速(PIV)测量瞬时流场结构，利用条件平均技术揭示近尾流的运动特性。下文由实验设置、结果、结论和讨论四个部分组成。

实验设置

实验在同济大学比例模型风洞(TUWT)进行。TUWT是一个亚音速，3/4开口闭环风洞，试验段长0.997米，宽0.433米，高0.283米，如图1(a)所示。最大流速为49m/s，收缩段出口纵向湍流强度小于0.5%，试验段轴向静压梯度小于0.005 Pa/m。使用的汽车模型是带车轮的1/12 MIRA比例模型，其全尺寸模型长4165mm，宽1625mm，高1421mm，本实验模型尺寸如图1（b）(c)所示。基于正投影面积，堵塞比为10.48%，来流流速为30m/s，由此得到基于车身长为特征长度的雷诺数Re=6.9e+5。模型由风洞地板下的四个空心圆柱支柱支撑在天平上，前保到喷口的距离为1.27H，来流方向定义为x正向，垂直地面为z方向，展向为y方向，如图1(a)所示。


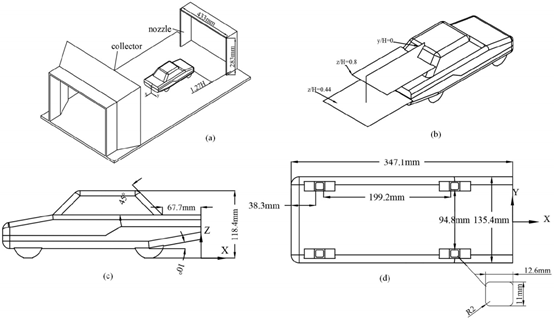
图1


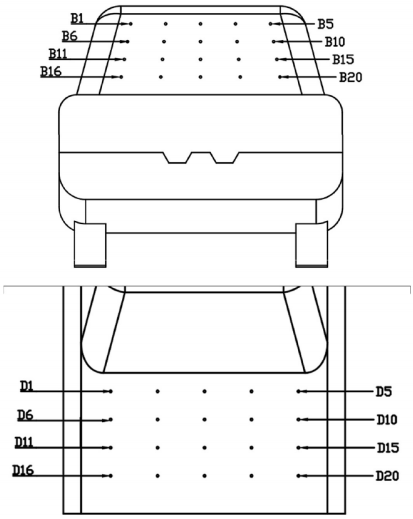
图2

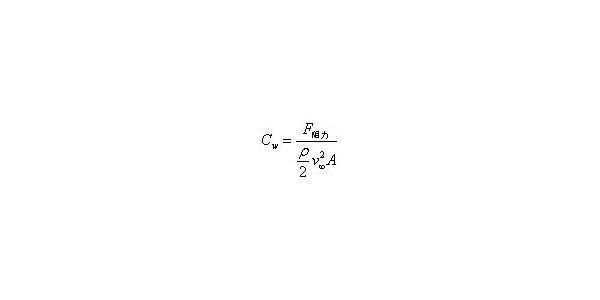
通过在模型表面的40个孔，使用24端口压力扫描仪来测量表面压力，扫描仪精度为±3 Pa，测量前每个端口都校准到精度0.001。如图2所示，背部和行李箱盖上分别分布着20个孔。550mm的乙烯管穿过模型的四个支撑点，减小对车底的流动的干扰。压力扫描仪每秒采集50个压力样本。总的采样时间是120秒，选择前20秒是为了清晰的观察到双稳态现象。压力系数Cp定义如下:



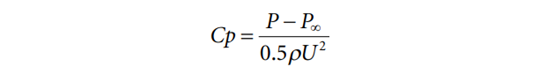
采用TSI PIV系统测量MIRA模型后的尾流。由玉米油产生的烟雾散部在整个流场，粒子直径约1-5 μm。流场由两个波长为532 nm的Vlite-500脉冲激光源照亮，每个脉冲最大输出能量为500 mJ，持续0.01μs。使用CCD相机记录下粒子图像。(PowerviewPlus 29 M型，双帧，6600像素×4400像素)。由610036激光脉冲同步器实现图像捕捉和流场照明之间的同步。在z/H = 0.8, z/H = 0.44的两个(x, y)平面和在y/H = 0的一个(x, z)平面进行了PIV测量，如图1(b)所示。使用互相关算法，询问区域为48 × 48像素，在两个方向上有50%的重叠，采样频率为1.5 Hz，采集了1200对图像来计算每个平面的时间平均流。

结果

1）背部瞬态压力

图3展示了前20秒背部的瞬时压力信号Cp。B1和B5是背部由上至下编号的第一行对称点，如图2所示。这对点的Cp值在-0.22和-0.30之间移动，如图3(a)所示。每个值的持续时间是随机的，最长大于2s，最短不大于1s。两个点是同时发生变化的。因此，在一种状态下，当B1为-0.22时，B5的Cp为-0.30，在另一种状态下，B5为-0.22,B1为-0.30，这种两种稳定状态就是双稳态现象，可能是背部后面后尾流的左右运动的转移形成的。


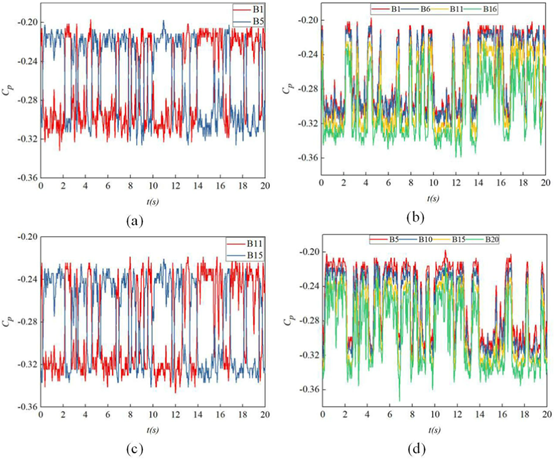
图3


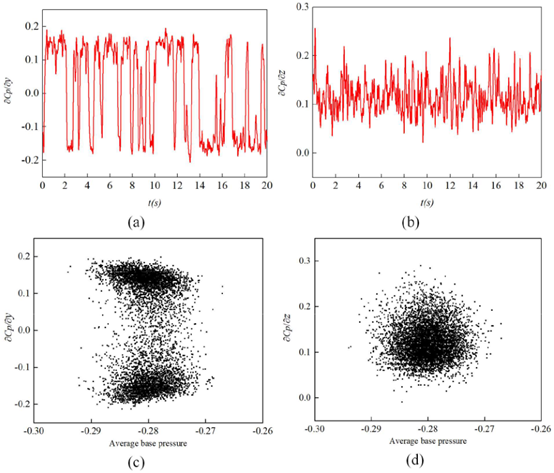
图4

B11、B15是位于背部第三排的另一对对称点，如图3(c)所示，此处也可以观察到同样的双稳态现象，但倾向值分别为-0.24和-0.32。在背部其他对称点的Cp波动也有同样的双稳态现象，此处没有列出。在图3(b)中，B1、B6、B11、B16为图2所示背部同侧点，压力变化是同步的，但倾向值不同。从图3(d)中可看出另一侧的点B5、B10、B15、B20也有同样现象。图4分别显示了背部展向的Cp梯度(∂Cp/∂y)和竖直方向的Cp梯度(∂Cp/∂z)，其定义如下：



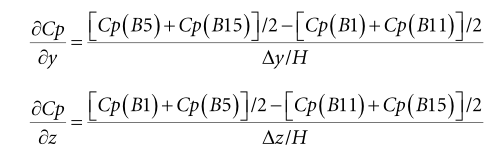
（∆y是 B1和B5之间的距离,∆z 是B1和B11之间的距离,H是模型的高度)展向Cp梯度图4 (a)在0.15和-0.15之间随时间跳动用,本文用P状态来表示∂Cp /∂y > 0的情况,∂Cp /∂y < 0的情况用 N状态来表示，∂Cp /∂y = 0为转换状态。当梯度值是-0.15时，背部压力从左到右递减。当梯度值为0.15时，压力变化趋势相反。因此，展向的压力梯度也表现出相同的双稳态现象，在两个倾向值之间移动，并在一段随机的时间内维持不变。图4(b)中垂向的Cp梯度在0.1上下波动，没有在两个倾向值之间移动，也没有持续，这说明着背部上方压力始终高于下方,没有双稳态现象。图4(c)和(d)分别显示了120s期间，所有样本的平均基压与∂Cp/∂y、∂Cp/∂z的关系。平均基压从-0.29到-0.27变化很小小,但∂Cp /∂y集中在两个值,一个值是0.15的P状态，另一个是-0.15的N状态,值为0附近的转换状态是在P和N状态切换中捕获到的信号。以0为中心的点比其他两个位置的点要少得多，说明P态和N态之间的切换非常快。然而，图4(d)中的∂Cp/∂z集中在0.1，没有出现两个不同的位置。为了更深入地了解压力信号，并清晰地了解每种双稳状态的基压，根据图4(a)中的压力梯度，将120秒的瞬时压力信号分为三组(∂Cp /∂y > 0.05 (P状态),-0.05 <∂Cp /∂y < 0.05(转换状态),∂Cp /∂y < -0.05 (N状态))。在图5(a)中，对于P状态，背部表面压力从右上角到左下角逐渐减小，而图5(b)中的N状态则正好相反。N态和P态的低压区主要位于背部两侧的下角。在图5(c)中，对于转换状态，压力几乎是对称的，与平均表面压力系数相同，如图5(d)所示。


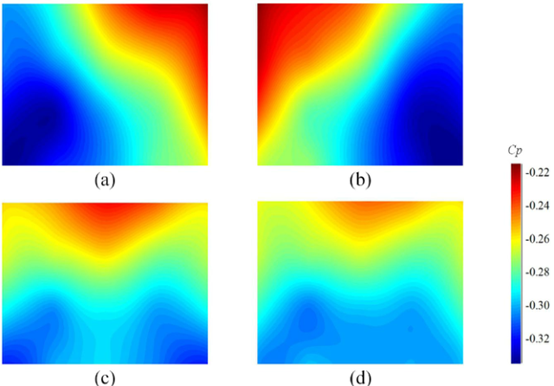
图5

2）行李箱盖的瞬态压力

图6显示了20秒内行李箱盖上的瞬时压力信号Cp。D1和D5的压力随时间变化基本相同，没有在两个倾向值之间变化，说明该位置没有双稳态现象。可能是因为背部与行李箱盖相交处出现横向涡,行李箱盖上最靠近背部的第一排孔被横向涡包裹着，因此横向涡对第一排孔板起到了屏蔽作用。D6、D10和D16、D20是图2所示的行李箱盖上的两对点，在背部仍然有图6(b)和(d)所示的双稳态现象。除第一行之外的所有对称点都有双稳态现象(本文没有列出所有对称点)。D6、D11、D16和D10、D15、D20分别为图2所示的行李箱盖两侧的点，行李箱盖同侧点的波动趋势相同，如图6(c)和(f)所示。平均Cp值在接近车顶后缘时增大，说明表层压力增大。从背部B1和行李箱盖上D16的波动线可以明显看出，它们从一个倾向值到另一个倾向值的移动时刻不同，意味着背部和行李箱盖上的双稳态不是同步的。图7显示了行李箱盖上沿展向的Cp梯度(∂Cp/∂y)，其定义如下:



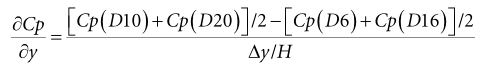
(∆y 是D6与D10之间的距离，H是模型高度)图7(a)和(b)展示了与背部看到的相同的双稳态现象，但是移动范围更小，说明背部的压力变化更强烈。图8为行李箱盖的条件平均压力等云图。如图8(a)所示，盖板P状态表面平均压力从左上角到右下角逐渐增大。图8(b)中的N状态则相反，低表面压力区位于行李箱盖的前部。在图8(c)的转换状态下，后备箱两侧的表面压力几乎是对称的，前部为低压区，后部为高压区。在图8(d)中，各状态的平均表面压力与转换状态相似，但左侧压力较高，这可能是由于N状态出现频率较高，持续时间较长所致。结合背部和行李箱盖的表面压力可以知道，车顶的后缘压力高,然后至背部与行李箱盖交界处逐渐降至最低值,最后到行李箱盖的后缘上升到最高值。


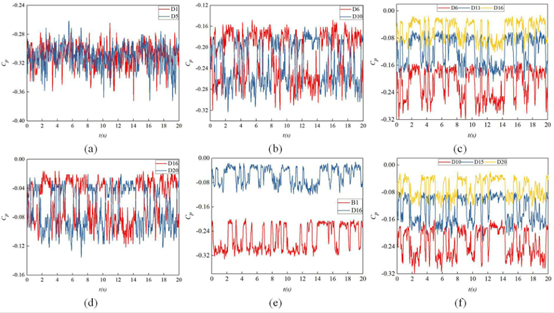
图6


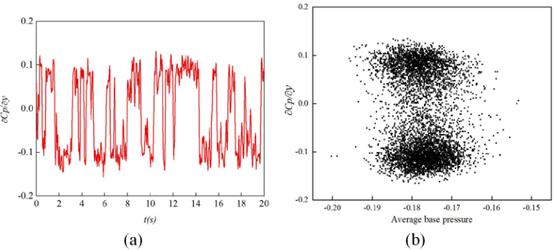
图7


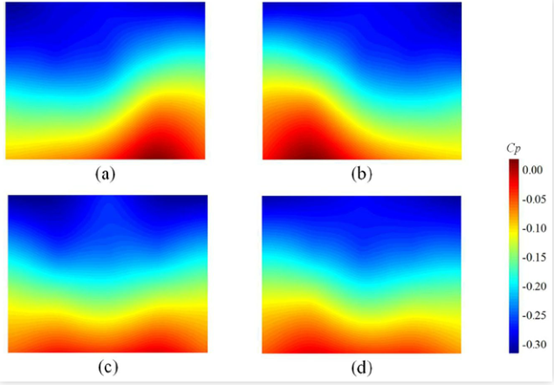
图8

3）尾流瞬时速度

基压特征是尾流运动的直接表现，因此本文主要讨论了MIRA比例模型的双稳态尾流结构。利用尾流的全局量来鉴别双稳态。由于它的演化过程时间比较长，因此可以用1.5 Hz的PIV测量进行分析。在z/H = 0.8的平面上，动量亏损重心（barycenter of momentum deficit）yb作为尾流位置的指标，定义为:



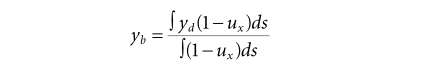
(yb是动量亏缺重心，yd = y/H，模型高度是H,ux = u/ U，实际流向速度u，初始速度U)，积分区间为ux < 1。因此，在PIV快照上动量亏损重心位置总是位于流动速度较低的一侧。图9为z/H = 0.8平面上瞬时流线图，转换状态动量亏损重心位置约为0，P状态的yb明显大于0,N状态的yb明显小于0。因此，可以通过尾流速度分布来区分尾流状态。在转换状态下可以看到两个大涡，其速度在y/H = 0的几乎是关于流向对称分布的。在P状态或N状态时，速度场向一侧倾斜，导致了如图5(a)&(b)和图8(a)&(b)所示的不对称压力云图。但是如图10，在z/H = 0.44平面上的瞬时速度流线图中没有观察到从尾流左到右摇摆，意味着在行李箱后没有出现双稳态现象。


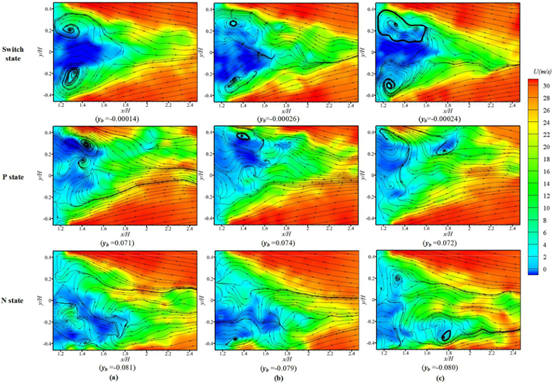
图9


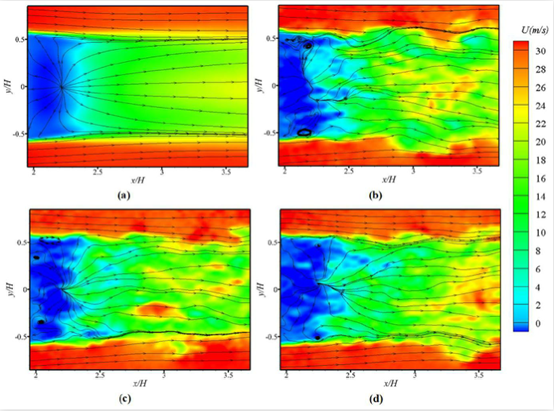
图10

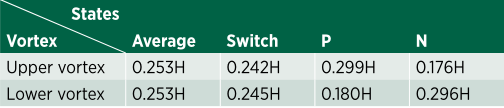
基于动量亏损重心yb，对z/H= 0.8平面尾流的瞬时速度场进行了条件平均，如图11所示。状态P和状态N对应的结果分别如图11(c)和(d)所示，且平均再循环流场不对称，离背部较远的涡旋远大于对侧的涡旋。但如图11(a)所示，所有状态的平均尾流与转换状态的平均尾流基本相似，均呈现对称分布。表1是根据图11给出的漩涡中心到背部的距离，表2是漩涡中心到流向轴y/H = 0的距离。图11(c)中P状态下对应上涡的大涡与背部和流向轴的距离分别为0.265H和0.299H，对应下涡的小涡与背部和流向轴的距离分别为0.192 2h和0.180H。在N状态下，图11(d)中低涡对应的大涡与背部和流向轴的距离分别为0.271 1h和0.296H，低涡对应的上涡对应的小涡与背部和流向轴的距离分别为0.199H和0.176H。因为它们的涡旋大小和到背部和流向轴的距离相差很小，可以推测，P态和N态对压力的影响几乎是相同的。此外,与所有状态的平均结果相比,转换状态涡心的到背部的距离较大,而流向轴心距离较小(见表1和2),这表明转换状态可能对背部和行李箱盖的压力贡献较小。此外，双稳态状态的改变可能会对侧向力产生影响，进而对操纵性有影响。然而，双稳态尾流现象与空气动力学之间的联系还没有被完全理解，需要进一步研究。图12为尾流在y/H = 0平面上的平均速度场和瞬时速度场。在图12(a)中，中段平均尾流在背部和顶盖上方出现一个大涡。此外，在行李箱基面后面可以看到一对反向旋转的涡对。流场从车顶后缘分离，然后撞向行李箱盖，再循环形成大涡，这可以解释为什么在第一行孔板上不存在双稳态现象。行李箱盖后的气流在尾缘分离，与底部气流相互作用形成了涡对，从瞬时尾流可以观察到背部后尾流的上下摆动，如图12(b)、(c)和(d)所示。此外，从图12(b)、(c)和(d)可以观察到行李箱盖后反向旋转涡对的交替脱落。


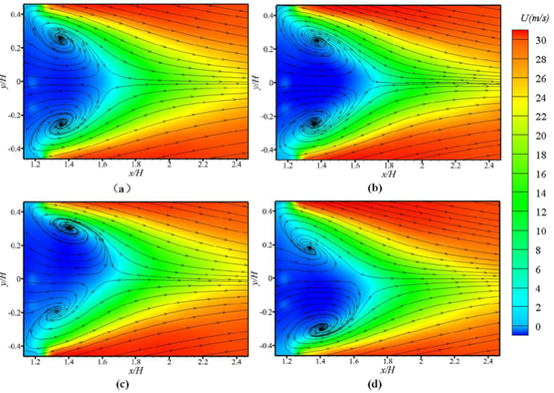
图11


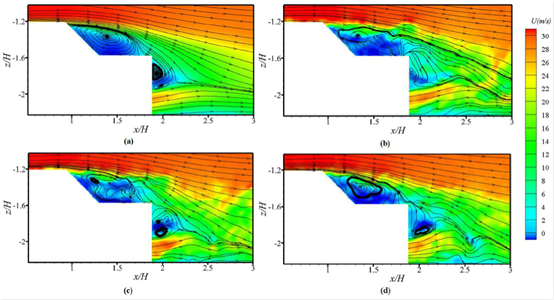
图12

表1


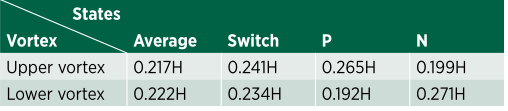
表2


结  论

基于阶背式1/12 MIRA模型长度，在雷诺数6.9+e5情况下对其尾流进行了研究。对背部和行李箱盖瞬时压力信号的分析均呈现双稳态现象，在展向上在两个倾向值之间转换。双稳态现象出现顺序是随机的，但其在背部和行李箱盖侧的同一侧的变换是同步的，但背部和行李箱盖二者之间并不同步。N状态和P状态的表面压力云图几乎对称。平均后尾流在z / H = 0.8平面出现了一对对称的大涡,这是长时间平均的结果并且不反映非定常流的结构。根据瞬时流场分析，回流区有对称破裂位置，这导致了尾流的数据统计后的对称，可能导致非定常侧力向，而在行李箱后不会出现双稳态现象。根据对涡位置的初步分析，抑制双稳态现象可能具有减小气动阻力，但还需要进一步证实。

讨  论

因为这种长时间尺度的行为已经在其他轴对称三维几何形状的尾流中观察到，双稳态现象可能是尾流紊流的一个重要特征。不对称状态P和N的共存非常依赖于实验设备的对称程度。此外，流场经过长时间平均后是统计对称的，所以在数值模拟中，只有在足够的物理时间下，才能看到非定常模型的双稳态行为。进一步工作将致力于双稳态对气动性能的影响。

文章来源：Yan, G., Xia, C., Zhou, H., Zhu, H. et al., "Experimental Investigation of the Bi-Stable Behavior in the Wake of a Notchback MIRA Model," SAE Technical Paper 2019-01-0663, 2019, https://doi.org/10.4271/2019-01-0663