摘要-众所周知,城市道路交叉口是交通事故的常发地,了解交叉路口的动态交通情况对于研究如何防止交通事故非常有必要。当自动驾驶车辆穿过交叉路口时,预测即将到来的其他车辆的轨迹是ADAS的要求。在本文中,我们提出了一种城市交叉路口转弯车辆轨迹预测方法。转弯机动车辆的轨迹预测比直行机动车辆更困难,因为转弯车辆在接近交叉路口时减速并且在离开交叉路口时加速。此外,速度的变化取决于诸如交叉角、拐角半径之类的因素。我们的方法生成了一种新的轨道预测所需的速度模型,该模型考虑了交叉口几何形状和其他车辆的观测速度。具体而言,我们假设人行横道附近的速度变得极小,并通过拟合过去的顺序速度和估计的最小速度到三次函数来计算速度模型。我们的方法的优点是能够预测在任何交点和任何位置的轨迹。该方法在实际交通场景中的预测性能优于其他方法。
作者: Atsushi Kawasaki and Tsuyoshi Tasaki
Ⅰ介绍
近年来,大量的主动安全驾驶系统和自动驾驶汽车被开发出来。这些驾驶系统需要保证驾驶员在动态变化的交通环境中的安全,并需要了解未来环境会发生什么变化。城市道路交叉口被认为是交通事故的常发地,了解城市十字路口的动态交通状况有助于预防乘客受伤。此外,在自动驾驶车辆的路径规划算法中,需要对交叉口交通参与者的长期轨迹进行预测。当自动驾驶车辆穿过十字路口时,需要对迎面而来的车辆进行预测。在诸如日本和英国这样的左手驾驶国家,对迎面而来的车辆进行轨迹预测的目标操作是直行和左转。然而,预测转弯车辆的轨迹是困难的,因为车辆经历了大的速度变化。转弯车辆在接近十字路口时减速,在离开十字路口时加速。此外,速度的变化取决于接近速度和交叉几何形状,包括交叉角度、道路宽度和拐角半径等因素。
沃尔夫曼、艾尔等人[ 1 ]分析并模拟了所有十字路口的车辆转弯行为,以进行驾驶模拟。他们构建了一个速度模型,用两个表示减速和加速的三次函数来表示。这些函数的系数被建模为正态分布,并通过最大似然法进行估计。然而,他们的模型仅用于模拟,并且难以应用于实际交通情况下的预测,因为速度模型只能从固定位置(进入十字路口的入口位置)生成。在轨迹预测中,必须能够在任何一个位置生成和更新模型。我们提出的方法是能够在任何交叉路口和任何位置转弯进行轨迹预测,并构建了一个新的期望速度模型,用于基于交会几何和观测速度的轨迹预测。假设速度在人行横道附近变得最小,我们通过拟合过去的连续速度和估计的最小速度来计算速度模型。我们在地图上定义速度变得最小的位置,并将这个位置称为“速度控制点”。此外,为了预测未来许多时间步长的轨迹,我们将我们期望的速度模型与扩展卡尔曼滤波器( EKF )相结合。实验是在真实环境中进行的。与传统方法相比,该预测方法可以提高状态预测性能。
Ⅱ相关工作
近年来,机器人[2]领域对交通轨迹预测问题进行了积极的研究。在[3]、[5]中,针对变道情况提出了基于车辆运动模型的预测方法,在[3],[4]中,轨迹分量被建模为五次多项式,卡尔曼滤波器已被广泛用于预测轨迹,同时考虑了车辆运动的不确定性[5],[6]。Kim et. al.[5]定义了变道和弯道所需的期望偏航率,并在EKF中加入了期望偏航率。此外,还提出了基于高斯混合模型[7]和蒙特卡罗模拟[8]的概率轨迹预测方法。
机器学习技术也被用于预测轨迹。通过高斯过程[9]学习车辆轨迹的模型参数。介绍了考虑车辆相互作用的更复杂的模型,包括耦合隐马尔可夫模型[11]和动态贝叶斯网络[10]。近年来,已经提出了使用深度神经网络的预测方法。在[12]中,动态占用网格图用作深度卷积网络的输入。在几种DNN架构中,递归神经网络被广泛用于学习顺序结构。Kim 等人[13] 将一系列车辆坐标输入到长期记忆中,并在占用网格地图上生成关于未来位置的概率信息。然而,这些机器学习方法依赖于训练数据,其缺点是无法预测未知环境下会发生什么。
对交叉口进行了专门的预测方法的重新开发。如第Ⅰ节所述,Wolfer-Mann [1]对车辆在任何路口转弯的行为进行了建模,但它们的模型是模拟的,不能从任何位置生成。特朗等人[9]利用高斯过程回归建立了转弯机动的速度模型。然而,它们的模型集中在一个交叉口的情况下,不能应用于任何一个交叉口。利布纳[14]还提出了一个考虑曲率的速度模型,可应用于任何交点。在上述工作的启发下,我们的目标是预测车辆在任何十字路口的转弯轨迹以及在实际环境中的任何位置。我们的方法通过使用更多的交叉口信息(如相交角、曲率半径、人行道的横向距离和人行横道的位置)来获得更好的性能。
III.系统概述
测量数据是从城市十字路口的真实交通场景中获取的。我们使用了一辆装有视觉传感器和360度激光雷达Velodyne HDL - 32e的实验车。激光雷达获取的原始数据以三维点云的形式存在。本文涉及的交叉口是四个道路交叉口,类型有人行横道,不涉及紧急交叉口或环形交叉口。
预测算法的输入主要有两种:1 )其他车辆状态,如位置、方位、速度、横摆角速度和加速度;2 )交叉口几何形状,例如二维轨迹图、相交角度、曲率半径和距人行道的横向距离。该状态是从车辆检测和跟踪系统获得的。检测和跟踪系统基于粒子滤波,其输入是3D点云数据。粒子滤波的可能性是通过基于[15]的点云拟合矩形来计算的。图1 ( b )示出了检测和跟踪系统的结果。二维轨迹图对应于每条迎面而来的车道和机动,由间隔1m的点序列组成。我们将点序列中的点称为“航路点”。地图由B样条曲线创建,B样条曲线的控制点是从交通参与者的地面真实位置中选择的。图6第二列中的黑点显示了轨迹图。此外,由于我们关注转弯车辆的轨迹预测,交通参与者的机动被认为是已知的。
图1( a )显示预测对象车辆的交通场景;( b )车辆检测和跟踪系统的结果;白色矩形显示自我车辆,青色矩形显示粒子过滤器的检测结果,黄色矩形显示地面真实情况。
预测算法生成交叉口转弯车辆所需的速度。此外,基于[ 5 ]产生期望的横摆角速度。通过将这些期望的模型和当前的其他车辆状态与EKF相结合来预测其他交通参与者的未来位置。预测状态每0.1s计算一次,到最大预测范围为4.0s,观察的时间步长也为0.1s,预测在每个时间步长进行。
IV. 转弯车辆轨迹预测
A.生成期望速度模型
为了预测转弯车辆的轨迹,我们生成了未来的期望速度。我们期望的速度模型由两个三次函数组成,它是用相交几何来生成的。为了解决无法从任何位置创建[ 1 ]的速度模型的问题,我们在地图中建立了速度控制点。速度控制点被定义为速度变得最小的位置。考虑到车辆和行人之间的相互作用,我们假设人行横道周围的速度变得最小。在本文中,速度控制点等于最靠近人行横道的航路点。图2显示了速度控制点和期望速度之间的空间关系。期望的速度模型被分成两部分,流入部分vin ( t )和流出部分vout ( t ),它们之间的边界被定义为车辆达到最小速度的时刻:
首先,我们重点讨论了vin(t)的计算方法。我们通过拟合观测到的过去的序列速度和估计的最小速度到三次函数来计算vin(t)。由于由跟踪系统观测到的交通参与者的当前速度是不稳定的,所以我们在1.0s周期内利用序列速度。此外,最小速度可以在[1]的基础上进行统计计算,但我们将其速度定义为拟合前的初始估计值vmin。我们通过最小三次函数与包含观测速度和vmin的速度之间的误差,将数据拟合成三次方程。图3示出了该装置的示意图。
初始最小速度v¯min综合了交叉口几何形状和驾驶员特征的影响,例如接近速度vint、交叉口角度θint、路缘半径rint和车辆在人行道出口处的横向距离lint。接近速度vint定义为[1]停车线上的速度。在本文中,vint是通过计算到达停止线时的速度来表示的,假设加速度恒定。假设vmin遵循正态分布,vmin根据经验估计为影响因素的线性函数,如下所示:
其中a1;…;a5是通过真实交通数据的最大似然估计来计算的,我们使用[ 1 ]中描述的参数。
此外,拟合需要在速度变得最小时对vin ( t )和tmin的初始估计。为了计算这些值,从速度控制点的约束条件中获得以下方程:
其中L是从当前车辆位置到速度控制点的路径长度。我们将vin(t)和tmin的初始估计定义为vin(t)和tmin (在下文中,过线显示了初步估计)。如果通信的状态参与者被准确观察到,C4;in和C3;in等于v0,a0即为当前时间的速度和加速度。然而,为了考虑观察误差,在估计步骤中C4;in和C3;in被定义为在在[vmin-3.0,vmin +3.0]和[-0.3G,0]范围内,其变化幅度分别为0.5; G表示重力加速度。C4;in的变化范围是根据观测速度误差的标准差来确定的,而C3;in的变化范围是基于舒适减速一般小于0.3G的证据确定的。对于tmin、C1;in和C2;in,方程( 1 )、( 4 )和( 5 )求解如下所示:
图2所示,速度控制点与期望速度的时空关系。
图3所示,期望速度的入流部分vin(t)的计算方法是将观测到的过去速度和初始最小速度vmin之间的差的平方残差之和与模型提供的拟合值进行最小化。
对于vin(t)和tmin,则为vin(t)和tmin(以下所示为初始估计)。如果准确观察交通参与者的状态,则c4;in和c3;in等于v0和a0,即当前时刻的速度和加速度。然而,为了考虑估算步骤中的观测误差,c4;in和c3;in被定义为在[vmin-3.0,vmin+3.0]和[+0.3G,0]范围内,变化幅度分别为0.5,G表示重力加速度。c4;in的变化范围是根据观察到的速度误差的标准差来确定的,c3;in的变化范围是根据舒适减速一般小于0.3G的证据来确定的。式(1)、(4)、(5)求解tmin、c1;in、c2;in过程如下:
当式(9)为c3;in和c4;in的最小变化量时,vin(t)设为vin(t)的初始估计值。
其中vobs由观测到的过去速度表示。
接下来,使用初始值vin(t)对三次函数vin(t)进行优化。根据速度控制点方程(4)、(5)的约束条件,将vin(t)中的c3;in、c4;in 移除 :
其中目标参数定义为C =
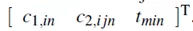
。残差的平方之和由下式得出:
其中w1和w2是权重。由于观测到的速度数较大,权重设为:w1 = 0.1;w2 = 1.0。
用迭代非线性高斯牛顿法对三次函数进行拟合:
其中et(C)是残差和J是雅可比矩阵
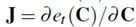
上标显示优化的迭代次数。在本文中,最大迭代为10。这将生成所需速度模型的流入部分。
接下来,我们解释了速度模型的流出部分。我们计算了vout(t),它通过vmin和法定速度vmax,在vmin和vmax处导数为零。未知变量C1;out和c2;out是通过[1]得到的。
接下来,我们解释速度模型的流出部分。我们计算通过vmin的vout (t)和法定速度vmax在vmin和vmax。通过使用[1]获得未知变量c1;out和c2; out。假设这些变量服从伽马分布。这些分布的参数也被估计为影响因素的线性函数,如交叉口的几何形状和法定的速度限制。









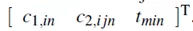 。残差的平方之和由下式得出:
。残差的平方之和由下式得出:

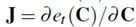 上标显示优化的迭代次数。在本文中,最大迭代为10。这将生成所需速度模型的流入部分。
上标显示优化的迭代次数。在本文中,最大迭代为10。这将生成所需速度模型的流入部分。  广告
广告 




 广告
广告