狭窄环境下牵引车-挂车系统基于环境和行为的搜索轨迹规划方法
编者按:本文针对牵引车-挂车系统在狭窄空间下的路径规划问题,提出了一种混合A*-跳点搜索(HA-JPS)路径规划器,旨在解决以往的路径规划方法无法兼顾可行性和实时性的问题。通过将混合A*算法和JPS算法相结合,使得规划器能在满足运动约束的同时保证实时性。在多个TTS配置和典型环境下进行了对比仿真实验,实验证明了所提出的算法在不损失完整性的前提下,可以大大提高路径求解的实时性。
本文译自:
《An Environmental and Behavioral-oriented Search-based Trajectory Planning Approach for Tractor-trailer System in Narrow Environment 》
文章来源:
2023 IEEE 26th International Conference on Intelligent Transportation Systems (ITSC) 24-28 September 2023. Bilbao, Bizkaia, Spain
作者:
Daiwei Li1,2, Liang Gao1,2, Bobo Jia1,2, Yi Yang1,2, Mengyin Fu1,2,3, and Shanshan Xie,1,2
作者单位:
1北京理工大学自动化学院,2北京理工大学自主智能无人系统国家重点实验室,3南京理工大学自动化学院
原文链接:
https://ieeexplore.ieee.org/abstract/document/10422548
摘要:牵引车-拖车系统(TTSs)由于其巨大的载货能力已被应用于物流和运输领域。轨迹规划在自动驾驶中起着重要的作用,现有的具有优势的规划通常是基于图搜索和采样的。然而,由于TTS独特的欠驱动特性和复杂的运动学约束,这种主流规划器存在实时性差的困难。基于TTS运动特性及其应用环境,提出了一种混合A* -跳点搜索(HA-JPS)规划器,其中JPS提高了规划器的实时性,而混合A*提供了运动约束的保证。为验证HA-JPS的规划效率、轨迹可行性和完整性,构建了若干TTS配置和典型环境。对比仿真实验结果表明,HA-JPS在不损失完整性的情况下,在不同场景下可将实时性提高50%以上。
1 引言
A.背景和动机
随着物流运输需求的不断增长,智能牵引挂车系统(TTS)的研究日益受到学者们的关注。TTS是由一辆动力牵引车辆(牵引车)和与其相连的多个无动力轮式平台(挂车)组成的连接结构[1]。TTS由于其诸多优点,被广泛应用于农业生产[2]、干线运输[3]、物流和货运[4]等各个领域。这些优点包括能够根据任务需要调整拖车的数量,具有高运输效率的大货物容量[5],以及与相同尺寸的刚体车辆(RBV)相比,具有更小的转弯半径,可以在狭窄的空间内灵活机动[6]。
然而,由于其欠驱动特性和铰链约束,TTS在运动规划方面提出了独特的挑战。目前流行的TTS运动规划是参考RBV规划,不太适合TTS规划。具体而言,TTS规划方法面临的挑战包括基于图搜索方法的维数诅咒,基于采样的方法对TTS模型约束考虑不足,以及在基于最优化的方法中需要平衡计算速度和求解质量。此外,铰链的存在会导致牵引车和拖车之间的速度不一致,从而导致折叠状态甚至侧翻现象。
总的来说,RBV中使用的运动规划方法对TTS的可移植性较低,因为每种规划方法都有其独特的优缺点。考虑到TTS的高状态维特性,TTS规划任务的优先级倾向于快速性,满足了基于搜索的规划器的核心思想。本文提出了一种专门针对TTS的轨迹规划方法,旨在提高TTS规划的实时性。混合A算法与跳点搜索(jump point search, JPS)算法相结合[7],实现TTS规划任务。通过有目的地修剪不必要的节点,优先探索与当前TTS状态取向角相同的方向,在开放和狭窄的环境中采用可变采样间隔,构建A -跳点搜索(HA-JPS)混合规划器,进一步增强搜索的方向性,从而提高搜索速度。传统混合A*与HA-JPS的主要区别如图1所示。
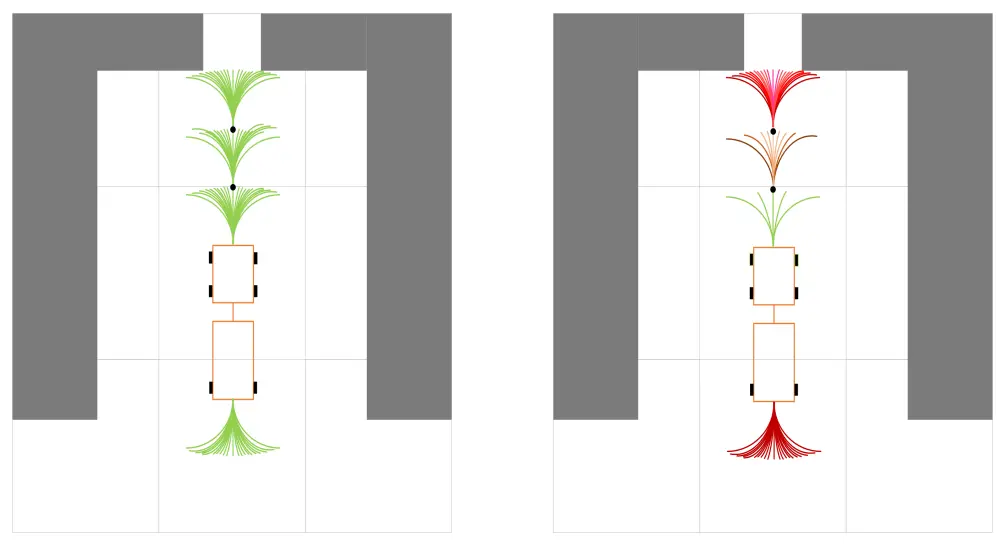
图1. Hybrid A*(左)和HA-JPS(右)的节点扩展模式比较:在开放或狭窄的环境中,修剪一些不需要的节点,可变采样间隔(将在第三节详细介绍)。
B.相关工作
RBV中主要的运动规划算法可以通过适当的修改在TTS中引用。主流的TTS规划技术根据其实现可分为四类:基于图搜索的、基于采样的、插值曲线的和基于优化的。此外,基于学习的方法作为一种新兴的技术,由于计算能力领域的进步而吸引了更多的关注。
基于图搜索的方法是一种确定性的方法,它将构型空间描绘成一个有节点和边的图,具有快速找到最优解的能力。典型的基于搜索的算法有Dijkstra[8]、A算法[9]和State lattice[10]。基于采样的方法通过对构型空间或状态空间进行随机采样,寻找其内部连通性,解决了确定性方法在高维空间中不能满足时间约束的问题[11]。其中,应用于TTS运动规划的具有代表性的基于采样的方法是概率路线图方法(PRM)[12]、快速拓展随机树 (RRT)及其变体(如闭环RRT[13]、Theta-RRT[14])。插值曲线方法通过拟合一组预定义的路径点来产生连续的光滑路径。
最被广泛认可的曲线插值方法是多项式曲线[15]。基于优化的方法将TTS规划任务作为最优控制问题(OCP),并对成本函数进行数值优化。在寻找最优数值解时,OCP可以表示为一个非线性规划(NLP)问题。通常使用内点法(IPM)[16]、随机分形搜索(SFS)[17]、顺序二次规划(SQP)[18]来求解优化问题。尽管基于优化的方法保证了规划轨迹的运动可行性和最优性,但其计算复杂度严格限制了在线规划的使用。为了缩小最优性与实时性之间的差距,最近的文献集中在多方法集成上,以提高实用性,将基于搜索或抽样的方法与基于优化的方法相结合[19]-[21],前者用于提供初始猜测,后者随着计算速度的逐步提高,将其收敛到局部最优。然而,现有的优化求解方法严格要求高质量的初始猜测,在一定程度上继承了这两种方法的缺点。
基于学习的方法揭示和建模数据中隐藏的和复杂的规律。[22]提出了一种终身学习框架,该框架将基于生成对抗网络(GAN)的轻量级模型与RRT相结合,以处理非线性动力学。提出了基于半监督学习的半卡车路径规划任务端到端学习[23],生成扫描面积最小的路径,避免与静态障碍物发生碰撞。然而,基于学习的方法通常依赖于现有的数据集,这些数据集必须涵盖TTS在特殊或困难情况下需要学习的所有内容。此外,主流的学习仿真软件(如Carla)不包含TTS模型,限制了基于学习的规划方法的发展。
2 牵引车-挂车系统模型
在工厂或货运物流环境中,TTS装载大量有效载荷且低速机动,因此车轮打滑效应可以忽略不计。TTS模型如图2所示,与经典的自行车模型类似,可以建立牵引车的运动学模型:

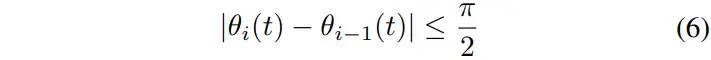
图2. TTS模型。
对于第个车身(),其轮轴的中点可计算为:
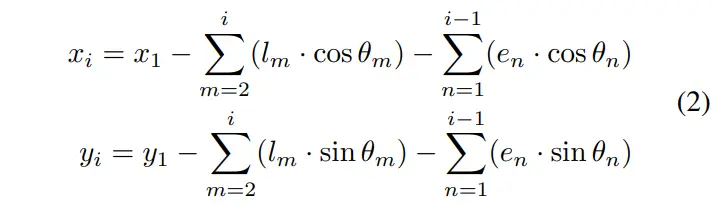
请注意,表示挂载偏移量,表示牵引车和拖车的轴距。根据TTS的挂载方式,可将其分为单轴模式()和离轴模式()两类,如果TTS为离轴模式,则可直接应用式(2);如果TTS为轴上或轴上/离轴集成模式,也可以通过将轴上模式指定为0来应用式(2),从而省去式(2)中包含的求和项。
第个物体的方向角和速度由[24]规定:
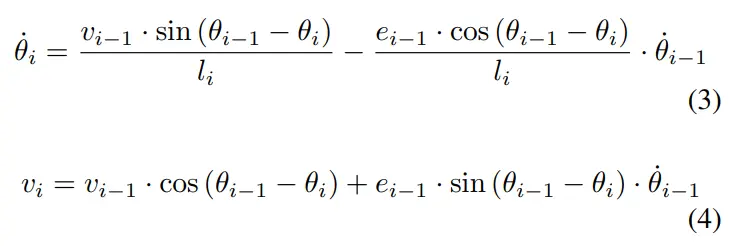
当状态变量, , 确定时,任意数量的拖车的状态可以用式(2)-式(4)来描述。
A.机械约束
牵引车-挂车系统具有内在的力学性能,反映在任意时刻的状态变量和控制变量的可行域:
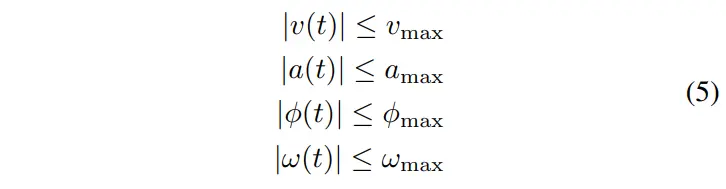
其中,、、分别表示牵引车的速度、加速度、转向角和转向速率的上限。另外,牵引车与第一挂车及相邻挂车的方位角差限制在90度以内,避免出现折叠现象:
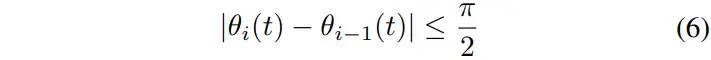
B.状态限制
确定TTS的初始状态和终端状态是运动规划的重要组成部分。通常,可以显式指定TTS第 个车体的初始状态:
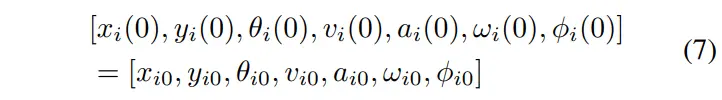
当TTS到达指定目的地,,时,其速度、加速度、转向速率均应为0,保证TTS稳定停车:
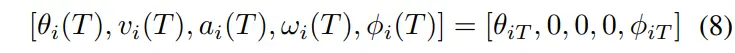
由于要求每辆拖车的朝向角严格符合期望朝向角是极其困难的,因此当拖车的实际朝向角与的差值小于某一阈值时,我们确定规划任务成功。但需要注意的是,牵引机的方向角是严格要求的,以满足期望值。此外,在、和已经返回0的条件下,转向角不限制为0。
 广告
广告 最新资讯
-
联合国汽车法规 R13:机动车制动统一批准规
2026-02-04 09:35
-
联合国汽车法规 R12:车辆碰撞中转向机构对
2026-02-04 09:34
-
联合国汽车法规 R11:机动车门锁与门保持件
2026-02-04 09:33
-
汽车指数最新批次测评结果发布:小米、岚图
2026-02-03 20:57
-
PHUD 真的不受管吗?——前方视野“透明区
2026-02-03 12:55





 广告
广告





























































