纯电动车整车各系统可靠度分解策略

0 引言

系统的可靠度与组成系统的关联零件的可靠度紧密相关，所以在系统的可靠度确定后，就需要把系统规定的可靠度指标合理地分配到关联的零件上，这需要调试过程也就是可靠度分配。

本文作者在整车可靠性目标确定后，基于各系统零件数量、安全件数量、复杂程度将整车可靠性指标值分解到系统总成，基于系统总成可靠性目标值再将可靠性指标分解到各零部件总成上，并对其进行适当修正，从而完成可靠性框架搭建。通过合理分配可靠度，提高汽车产品的可靠性。

1理论介绍

失效率，又称故障率。它是指产品在规定条件下，在规定时间内，完成规定功能的时候，产品的故障总数与寿命单位总数之比率，用λ(t)表示。用户使用汽车实现功能，在实现功能的过程中故障率曲线多呈浴盆状，因此又常将故障率曲线称为浴盆曲线。如图2所示故障率曲线可将故障分为3个时期:早期失效期、偶然失效期和耗损失效期。


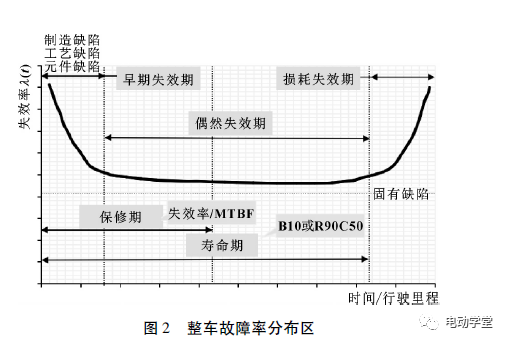
(1)早期失效期。因为产品中有不合格产品，故障率较高，但随时间的推移，不合格品被淘汰，故障率逐渐下降。加强产品生产过程中的质量管理，提高装配质量，是提高早期故障期可靠性的有效措施。

(2)偶然失效期。故障率低且稳定，发生故障是偶然的，何时发生也无法预测，因此提高此期间的可靠性也无具体措施。

(3)耗损失效期。产品已接近或达到设计寿命，随时间的增长，故障率明显增加。提高此时期内整个系统的可靠性，就必须在进入耗损故障期之前更换零件。

我国《汽车产品质量检验评定办法》中对故障是按其造成整车致命损伤(人身重大伤亡及汽车严重损坏)的可能性(概率)进行简单分类的。规定致命损伤概率接近1的称为致命故障;概率接近0.5的称为严重故障;概率接近0.1的称为一般故障;概率接近0的称为轻微故障或安全故障。故障分类的具体规定详见表1。


可靠度基本要求

在汽车可靠度分配过程中，由于其零件规模巨大且相互联系，必须建立统一的可靠性要求，单纯考虑可靠度而不考虑置信度，会增加分配可靠度的困难，而且容易造成混乱。目前行业主流方法是整车置信度统一，专注于可靠度的提升，推荐C50或C70。

在保证整车所有系统及零件总成置信度统一的条件下，汽车产品的可靠度还遵循两点分配原则，其流程如图3所示。


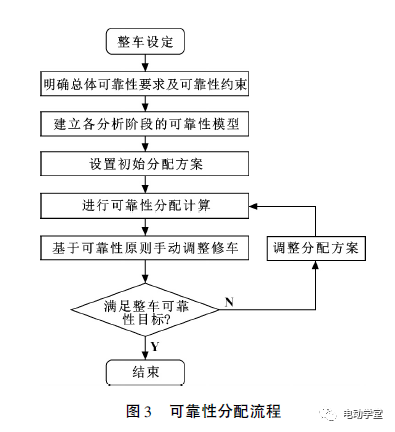
(1)层次清晰:元件/零件＞子系统/总成＞系统/大系统＞整车。

(2)关注零件要明确:安全件＞法规件＞一般件。

如元件/零件(Ｒ99C50)＞子系统/总成(Ｒ95C50)＞系统/大系统(Ｒ95C50)＞整车(Ｒ90C50);安全件(Ｒ99.8C50)＞法规件(Ｒ99.5C50)＞一般件(Ｒ99C50)。

2 整车可靠性分解

2.1 系统可靠度

一个系统是多个零件、部件、子系统或装配件构成的，完成期望的功能，并具有可接受的性能、功能和可靠性水平的一种特定设计。

2.2 整车系统划分

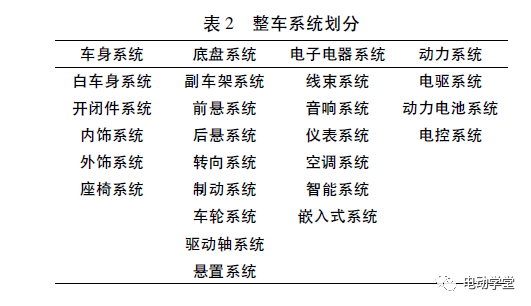
汽车各系统中，选择关键单元，先分解系统，再组合计算。各企业根据整车框架，对整车系统进行适当调整。为了更好地下达指标要求，建议划分到责任人身上，方便后期的可靠度验证。同时，关注全新技术的开发，满足客户需求。系统划分不宜过多，表2是某企业的整车系统划分。



2.3 绘制产品的可靠性框图

为了提高可靠性框图的规范性和可读性，需要遵守以下的一般性约定。

首先，不能将同一个产品的“可靠性框图”与“组成(或原理)方框图”混为一谈。“可靠性框图”描述的是系统与其组成零件，以及零件与零件之间的可靠性逻辑关系，位于同一(可靠性)串联支路中的各零件的相对位置没有任何物理意义，只表明其中的任一零件故障，是该串联支路故障，因此前后次序无关要紧。而“组成(或原理)方框图”描述的是系统与其组成零件，以及零件与零件之间的物理关系，或者说是“功能关系”，即使位于同一(物理)串联支路中，各零件的前后次序也不能随意变更。

对于大型复杂整车而言，建模过程应从系统级开始，自上而下逐步展开。假设，某可靠性框图由3个单元串联而成，如图4(a)所示;由3个单元并联而成，如图4(b)所示。


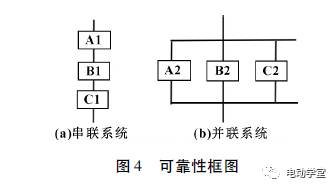
各串联子系统如图4(a)所示，可靠性最差的零件或装配件对系统的可靠性影响最大，且系统内组件增加，可靠度水平会逐步降低，可靠度计算方法:Ｒ1=ＲA1ＲB1ＲC1。

各并联子系统如图4(b)所示，并联条件下，系统可靠度随着组件数增加，对单一组件的可靠度依赖越来越小，可靠度计算方法:Ｒ2=1－(1－ＲA2)(1－ＲB2)(1－ＲC2)。

在建立可靠性模型时，通常假设产品的所有输入量均在规定的范围之内，即不考虑由于输入错误而导致系统故障的情况。

2.4 整车可靠性分配

在完成可靠性框图的绘制之后，可根据可靠性框图展示的逻辑关系推导出系统可靠性值的计算公式，即系统的可靠性数学模型。可靠性数学模型描述的是各单元的可靠性变量与系统可靠性值之间的定量关系，利用已知的单元可靠性值(如可靠度、失效率或者MTBF等)就能计算出系统的可靠性值。本文作者采用重要度、复杂度、技术水平、工作时间、环境因子分值计算方式进行计算，对搭建汽车可靠度有重要参考意义。

所谓可靠性分配，就是把系统(整机产品)的可靠性指标逐级向下，分解成各级组成单元的可靠性指标，是一个自上而下的分解过程。其整车统一置信度为C50，可靠度目标Ｒ90，该车型在行驶8年或16×104km后的系统可靠性分配如表3所示。


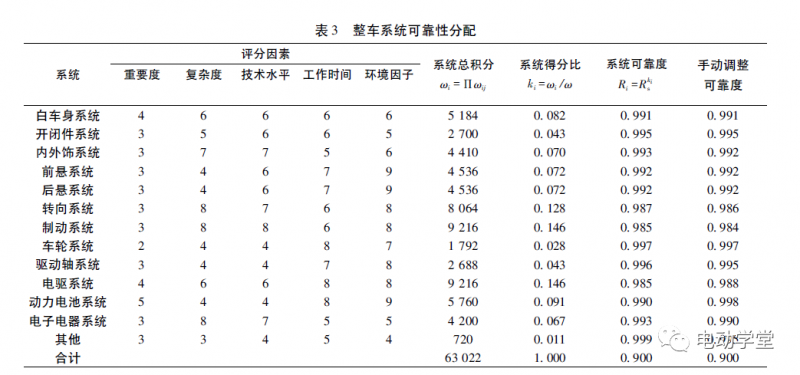
(1)系统积分=重要度×复杂度×技术水平×工作时间×环境因子。

(2)系统得分比=系统积分/系统总积分。

(3)系统可靠度Ｒi=Ｒs。

(4)最后手动修正可靠度。

在产品的方案论证阶段，有很多因素是未知的，或者是不确定的。因此，可靠性分配很难做到“精准”，只能将整机产品的可靠性指标“粗略”地分配下去。随着研制工作的不断深入，各种数据资料的不断增多，应该不失时机地对已分配的指标进行适当的修正和调整。另外，在进行可靠性预计时，可能会发现分配的指标不够合理，这也需要进行调整。因此，可靠性分配很难做到“一锤定音”，而是一个由粗到精、逐步趋于合理(相对合理)的过程。

同时，将系统产品的重要度水平分成等级，然后按照重要度、复杂程度等级手工修正可靠度。系统产品可靠度水平等级如表4所示。


同时，修正系统产品的可靠度水平等级，需要对它们出现的故障或失效后产生的后果进行评估，而这种评估存在着很大的模糊性，这就要求对技术水平、工作时间、环境因子也进行评估。

3 子系统分解

3.1 前悬麦弗逊系统

麦弗逊式独立悬架是众多悬挂系统中的一种，将白车身与车轮连接起来的具有弹性功能的系统，它的结构尺寸、布置方式、性能参数等与汽车的驾驶舒适性和操纵稳定性息息相关。它以结构简单、容易布置、研发成本低廉、舒适性尚可的优点赢得了广泛的市场应用。

通过对麦弗逊式悬架系统的可靠性框图进行研究，结合麦弗逊式悬架系统的结构分析，常用的麦弗逊悬架系统是一种混联系统。可靠性框图中具有串联零件、并联零件、混联零件。其中，减震器与螺旋弹簧并联，然后与横向稳定杆组成串联，再与转向节总成串联，同时三角控制臂、衬套串联后与轮胎并联、与转向节总成呈串联，左右悬架系统间是一种并联关系，最终得到可靠性框图，如图5所示。



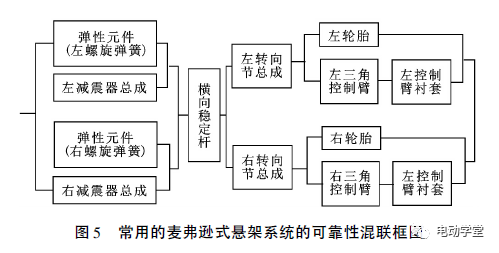
根据图5中各零件、总成的相互可读性关系网，系统分配到减震器、螺旋弹簧、横向稳定杆、转向节总成、三角控制臂、轮胎的可靠度分别为ＲA、ＲB、ＲC、ＲD、ＲE、ＲF，从而计算出调试后的麦弗逊式悬架系统的可靠度为Ｒ99.2=［2(ＲA+ＲB－ＲA ＲB)－(ＲA+ＲB－ＲA ＲB)2］ＲC［2ＲD(ＲE+ＲF－ＲE ＲF)－Ｒ2D(ＲE+ＲF－ＲE ＲF)2］。

根据可靠度定义，产品在规定的条件下和规定的时间内，完成规定功能的可信概率。由图6可知，麦弗逊式悬架系统在1×104km之内可靠度为Ｒ99.9C50;在1×105km时，可靠度约Ｒ97C50;在16×104km时，可靠度为Ｒ95C50;行驶里程超过16×104km之后，悬架系统可靠度随时间增加而降低，发生故障频率次数增多，可靠性变差。

目前验证悬架系统的可靠度要求，通常用多通道试验台架进行验证。为达到Ｒ99.2C50要求，通过威布尔计算出等效试验样本数量及寿命要求，如表5所示。

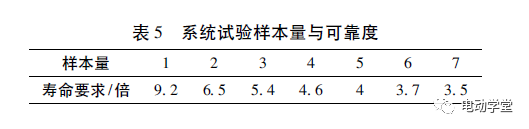
试验的可靠度由试验样品数及置信度水平，其关系为



式中:Ｒ为要求达到的试验可靠度;C为置信水平;N为试验样本数。

3.2 制动系统

制动系统的主要功能是汽车行车或转向时的主动安全措施。汽车行驶中如需要停下车辆，需要通过制动系统阻止轮胎滚动，停止后需要通过手刹锁死汽车车轮与变速器，避免偶然外力推动汽车运动。制动系统基本组成有4个部分，即功能装置、控制装置、传动装置和制动器。

制动系统失效主要有2种:

(1)关联失效。由于组成制动系统的各个零件、装配件的故障所引起的系统失效。

(2)环境失效。由于轮胎与地面附着阻力条件不良所引起制动失效，也就是刹车不灵或者刹车距离比较长，不能在短距离内把车停下来。这2种失效在起因和影响制动两方面都是大不相同的。关联失效可能是由于制动系统零件、装配件的功能策略丧失，或者功能达不到满足要求的部分失效，制动系统仍然可以正常工作。外部失效情况比较复杂，它是由于车轮与地面的附着阻力不良造成的刹车不灵或者刹车距离比较长的故障。

根据制动系统失效关系，设前制动失效、前左侧制动失效、前右侧制动失效、后制动失效、后左侧制动失效、后右侧制动失效的可靠度分别为Ｒ1、Ｒ2、Ｒ3、Ｒ4、Ｒ5、Ｒ6，如图7所示。制动系统的可靠度为:Ｒ98.4=1－(1－Ｒ1)·(1－Ｒ4)=1－［(1－Ｒ2)·(1－Ｒ3)］·［(1－Ｒ5)·(1－Ｒ6)］，最终得到制动系统各个总成零部件的可靠度。


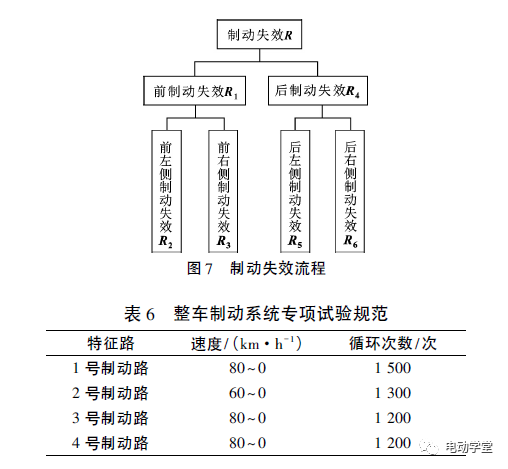
制动系统的可靠度验证，除了通过其零部件总成的可靠度进行Ｒ98.4C50要求验证，还可以用整车底盘专项试验验证制动系统可靠度，如表6所示，该循环次数等效3倍整车级8年或16×104km要求，通过威布尔理论计算得出试验样车为4辆车。

4 结论

本文作者根据整车Ｒ90C50的可靠度目标，基于系统重要度、复杂度、技术水平、工作时间、环境因子评估并分解可靠度到各个子系统上。根据系统或零部件总成可靠度，运用威布尔理论计算分析，获取最优样本量或加载零部件总成的寿命。

整车可靠度不仅仅是由子系统、零件总成可靠度决定，驾驶者的操作对可靠度的影响也很大;有些系统级试验台架费用昂贵，可以通过整车专项试验进行可靠度评估。

可靠性开发工程科学的分析方法已经在汽车研发设计中得到广泛应用，是汽车安全设计、寿命要求的关键指标要素，但是仍然有许多工作有待进一步改进。