基于线控制动系统的车辆横摆稳定性优化控制

本文对带有线控制动系统（Brake By Wire，BBW）的车辆进行研究，提出了一种横摆稳定性优化控制策略。以二自由度单轨车辆模型为参考模型，利用比例-积分（Proportiona-Integral，PI）控制算法求出附加横摆力矩。

由所计算出的车辆附加横摆力矩、方向盘转角来识别驾驶员转向意图和车辆实际行驶特性，通过广义逆法和数学归划法相结合的方法将附加横摆力矩分配到作用车轮上，由线控制动系统采用主缸定频调压法对各轮缸的目标液压力进行跟踪控制。

硬件在环试验结果表明，该控制策略能够有效地保证车辆在高附和低附路面工况下的横摆稳定性。

本文来自 2017 年 5 月出版的《 同济大学学报（自然科学版）》，作者是同济大学汽车学院与同济大学智能型新能源汽车协同创新中心的韩伟博士、熊璐教授、侯一萌和余卓平教授。

随着汽车电控系统的增多以及底盘集成化趋势的发展，传统液压制动系统受限于其自身硬件结构，已经无法满足制动系统发展的需求，并制约了车辆制动性能的进一步提高口 [1]。同时，新能源汽车，特别是纯电动汽车的推广和普及，也对制动系统提出了新的需求。结合线控技术和汽车制动系统而形成的线控制动系统较好地满足了现代汽车对制动系统发展的新需求，将逐渐取代现有的液压制动系统，成为未来汽车制动系统发展的趋势 [1]。本文所研究的内容及相关试验研究是在文献 [2] 中设计的线控制动系统的基础上进行的。

传统车辆横摆稳定性控制（Yaw Stability Control，YSC）的实现多采用分层结构：

上层为运动跟踪层，主要包括参考模型的选取和横摆力矩控制器的设计；
下层为转矩分配层，根据系统的优化目标和约束将所需横摆力矩合理分配给各执行器 [3]。

运动跟踪层中建立的参考模型根据驾驶员方向盘输入信号并结合车辆状态信息得到控制变量的参考目标值，一般选取横摆角速度或质心侧偏角作为控制变量 [4]。

文献 [5-6] 采用的线性二自由度车辆模型是多数驾驶员熟悉的车辆特性，反映了车辆线性区域的响应。由线性二自由度车辆模型得到的理想的横摆角速度及质心侧偏角对前轮转角均是二阶系统的传递特性[7]。

文献 [8] 同样采用线性二自由度车辆模型，并利用一阶系统替代复杂的车辆动力学方程，从而达到简化参考模型的目的。文献 [9] 则不考虑参考模型动态响应，只用横摆角速度稳态响应设计参考模型。在控制算法方面，根据理想车辆参考模型给出的结果，结合车辆驾驶员的当前操作状态和实际车辆状态，计算出要实现车辆理想状态需补偿给车辆的横摆力矩。

文献 [10-11] 采用比例一积分（Proportional-Integral，PI）控制，控制器设计关键是 PI 参数的选取。文献 [12-13] 利用最优控制方法实现反馈控制，设计线性最优二次型调节器（LQR），设定目标函数并使之达到最小。

下层转矩分配方法总体上可分为线性控制分配 [14-18]、非线性控制分配 [19-21]、动态控制分配 [14-15, 22]。其中，

线性控制分配是指执行器的输出与广义力的需求之间是线性关系，主要包括直接分配（direct allocation）[14]、链式递增法（daisy chaining）[15-16|、广义逆法 [17-18] 等。
非线性控制分配方法通过设定优化目标和不等式约束得到分配结果，精度高，但实时性差，主要包括二次规划法 [19-20]、加权最小二乘法 [21]。

基于电子液压制动系统的车辆稳定性控制多是通过单轮差动制动将计算出的附加横摆力矩分配至作用车轮 [23-24]，故可以借鉴传统 YSC 分配的方法以提高基于 BBW 的 YSC 性能。

轮缸液压力控制是 BBW 系统的核心，其控制性能好坏是上层 YSC 能否改善车辆稳定性的关键要素。在该方面国内外相关研究机构也做了大量研究：

文献 [25] 采用基于比例一积分一微分（Proportiona-Integral-Derivative，PID）控制算法的轮缸压力控制。
文献 [26] 采用模糊控制算法对轮缸压力进行控制。实车测试表明，对于 25 km/h 以内的速度信号跟踪，车内乘员感受不到实际车速的微小变化。
文献 [27] 通过建立液压系统的模型和反模型对液压力进行了有效控制。
文献 [28] 基于一体式制动主缸的电液复合制动系统提出了数表插值法和阶梯法并行的分段压力估算方法，能够准确地控制轮缸制动压力。
文献 [29] 采用轮询调度（round-robin scheduling）算法调节轮缸液压力，仿真表明系统的响应时间和控制精度对于车辆应用是可行的。

本文针对所提出的线控制动系统设计了新型控制策略，以实现装备该系统的车辆的稳定性控制功能：

首先描述了系统结构、工作原理和试验台架。
横摆力矩控制包括基于线性二自由度参考模型得到参考横摆角速度值；设计横摆力矩控制器，以参考横摆角速度与实际横摆角速度的差值为控制器输人，得到应补偿的横摆力矩值。
在转矩优化分配控制方面，通过基于广义逆法和数学归纳法相结合的方法得到各车轮的轮缸目标液压力值。
然后设计基于主缸定频调压法的轮缸压力跟踪控制方法，以快速精确地跟踪目标轮缸压力。
最后通过硬件在环台架试验验证算法的有效性。


1. 线控制动系统描述

1.1 系统结构和工作原理



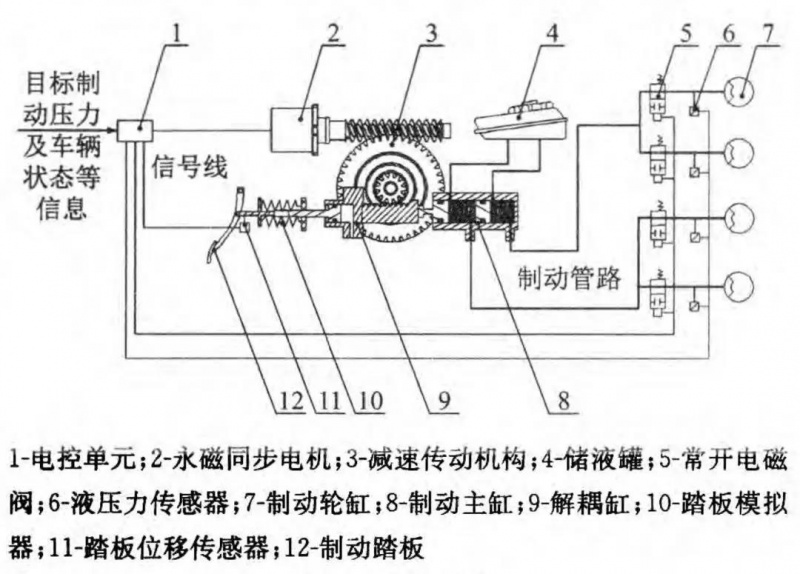
图 1 系统结构

所采用的线控制动系统的结构如图 1 所示。

在常规制动时，踏板位移传感器获得踏板位移，电控单元（Electric Control Unit，ECU）识别驾驶员的制动意图，并计算得到此次制动中所需的液压制动力大小。然后 ECU 通过控制电机驱动减速传动机构，减速传动机构推动主缸第一腔活塞推杆移动，进而推动主缸建立压力。

常规制动时电磁阀没有上电而开启，所以制动液经过液压管路通过电磁阀流向各轮缸产生制动力。由于解耦缸中的空行程断开了主缸推杆与踏板推杆的机械连接，所以制动踏板能够与主缸解耦。而踏板模拟器能够根据踏板位移反馈踏板力，提供良好的踏板感觉。

当 YSC 功能实现时，ECU 根据目标轮缸压力通过轮缸压力跟踪控制算法得到各电磁阀的控制信号，再通过液压力传感器的信号反馈，实现目标轮缸压力精确控制。

1.2 系统试验台架



图 2 系统试验台架

基于上文所述的系统结构和工作原理，开发了一套车辆稳定性控制研究硬件在环试验台架。如图 2、图 3 所示，硬件部分包括系统实物、控制器、主缸、轮缸、线束等。



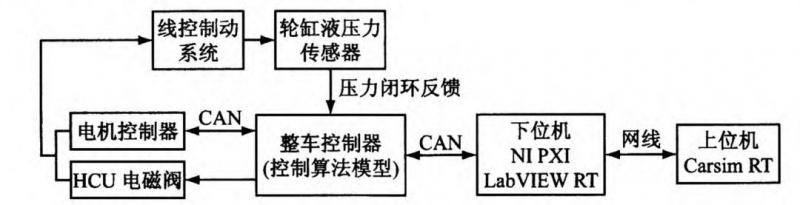
图 3 系统试验台架拓扑图

采用某型号工作站作为实时控制平台（即上位机）。在上位机的 Carsim/RT 软件中搭建整车模型。采用 NI/PXI 某型号机箱作为下位机。上下位机通过以太网连接。控制策略在 Matlab/Simulink 软件中建立。各模块之间采用控制器局域网络（Controller Area Network，CAN）通信，传递控制指令或传感器信号等。

2. 车辆稳定性优化控制



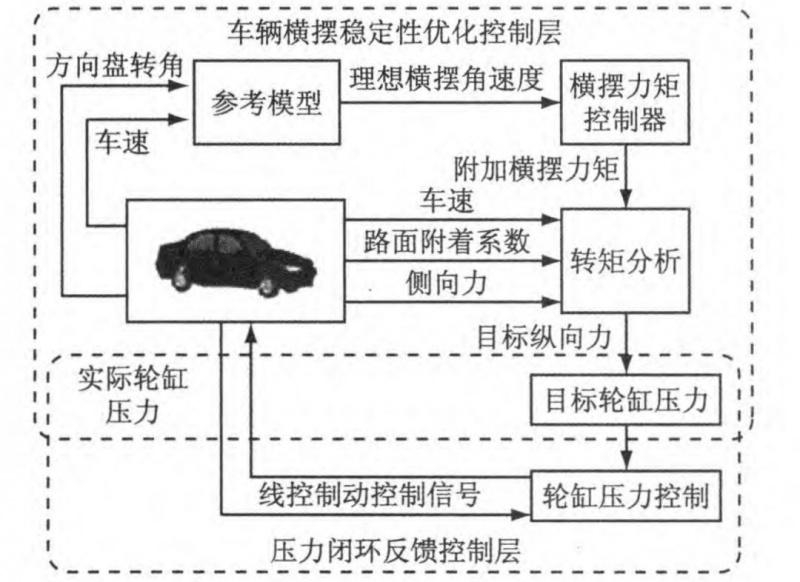
图 4 车辆横摆稳定性优化控制框图

在实现 YSC 功能时采用分层控制的方法，如图 4 所示：

首先由车辆参考模型获知当前车辆状态下的理想横摆角速度，继而设计横摆力矩控制器求当前车辆要维持车辆稳定状态所需的横摆力矩；
再将该横摆力矩输入给转矩控制分配模块，转矩分配控制模块能够根据车辆的速度、路面附着系数、轮胎侧向力等参数将所需横摆力矩转化为各车轮的需求制动力；
最后将各车轮的需求制动力通过计算转化为实际作用于车辆的液压制动力，即获得目标轮缸压力；
轮缸压力控制模块根据目标轮缸压力和实际轮缸压力进行闭环控制，最终实现 YSC 功能。


2.1 横摆力矩控制

2.1.1 参考模型选取及控制变量理想值的计算



图 5 线性二自由度车辆模型

以经典的线性二自由度车辆模型作为参考模型，如图 5 所示，图中 C_G 为车辆质心；V 为车辆质心处的车速，m/s；V_f 为前轮轮速，m/s；V_fr，为后轮轮速，m/s；l_f 为前轴到质心处的距离，l_f = 1.167 m；l_r 为后轴到质心处的距离，l_r = 1.233 m；β 为车辆的质心侧偏角，rad；Ψ 为车辆的横摆角，rad；δ 为车辆的前轮转角，rad。

该模型忽略了车辆的悬架系统，只考虑整车侧向及横摆运动，输出车辆理想的横摆角速度。根据牛顿第二定律建立车辆平面运动的动力学微分方程 [30]，如式 (1) 和 (2) 所示：



另外，在车辆具有高横摆角速度的情况下，当路面不能够提供足够的附着力时，此时根据式 (3) 来计算理想横摆力矩是不安全的。应该对横摆角速度设定上限或l，即式 (4) 所示：



式中：μ 为路面附着系数；g 为重力加速度，g = 9.8 m/s。修正理想横摆角速度如式 (5) 所示：



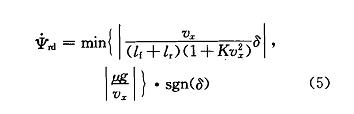
2.1.2 横摆力矩控制算法设计

横摆力矩控制器的设计采用工程上常用的 PI 控制方法，将理想横摆角速度与实际横摆角速度的偏差作为控制器输入 e(t) ，t 为时间，依据以下控制律得到 M_D：




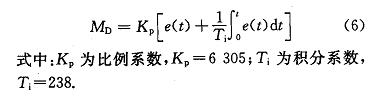
2.2 转矩优化分配控制

2.2.1 分配对象的选取

车辆稳定性控制所需的附加横摆力矩是通过线控制动系统调节 4 个轮缸制动压力来实现。由于车辆的外前轮和内后轮是影响车辆横摆力矩效率最高的 2 个车轮，而对内前轮和外后轮制动时虽然获得的车辆横摆力矩较小，但仍然能产生一定的修正作用。

因此，在进行转矩分配时同时控制同侧前后轮，即：

当车辆处于不足转向时，控制内后轮和内前轮产生制动力，得到正的附加横摆力矩使车辆回到稳定状态；
当车辆处于过多转向时，控制外前轮和外后轮产生制动力，得到负的附加横摆力矩使车辆回到稳定状态（如表 1）。

表 1 转矩优化分配对象的选取



2.2.2 分配算法的设计

根据附加横摆力矩和方向盘转角选取了分配对象，为了确定各作用对象应该分配的制动力矩，需要对转矩分配算法进行设计。

控制分配问题一般可以描述为：



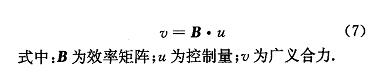
从分配算法的选择、优化目标的选择、分配算法的计算 3 个方面进行转矩优化分配方法的设计。

2.2.2.1 分配算法的选择

采用广义逆法和数学规划法相结合的方法进行转矩优化分配。

广义逆法是从控制分配问题的数学角度考虑，如果能求出 B 的逆矩阵，问题则得到解决，但是 B 通常不是方阵，其逆矩阵并不存在，因而顺着这个思路提出广义逆法（Pseudo Inverse Method）。由于矩阵 B 的维数通常是 m < n，则 v = B·u 为超定方程，理论上有很多组解，在 B 为满秩矩阵时，有：



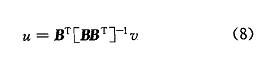
将取控制量的二范数为优化目标从而得到式 (8) 所描述的最小二乘解。

利用计算机求解广义逆法是很简单高效的，但该方法并不能很好地考虑实际中存在的约束，而仅仅从数学层面解决问题，因此往往采用改进的广义逆法通过迭代使解始终在约束范围内。

有关约束范围内的求解问题通过数学规划法来解决。数学规划法包括目标函数、等式约束和不等式约束。若目标函数为一次、约束条件为线性，该数学规划是线性规划（Linear Programming）；若目标函数为二次、约束条件为线性，该数学规划是二次规划（Quadratic Programming）。

本文采用二次规划法进行求解。二次规划可以在有限步内求解，还可以方便地转化为序列最小二乘（Sequential Least-Squares，SLS）和加权最小二乘（Weighted Least-Squares，WLS）问题，加快求解速度。

基于以上分析，将广义逆法与数学规划法结合起来设计转矩分配方法，既便于计算机求解，又能较好地处理约束条件。

2.2.2.2 优化目标的选择

考虑车辆所受的广义力（本文中为横摆力矩）在 4 个车轮之间如何分配最合理这一问题时需要选择一个优化目标。文献 [19-20] 提出轮胎利用率这一概念，表述为单个轮胎上的路面附着力与所能获得的最大附着力的比值，如式 (9) 所示：



日本学者 Abe 等 [31-32] 提出以所有轮胎利用率平方和最小为目标函数分配广义力。目标函数如下式所示：



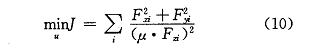
考虑到侧向力受限于实际条件不可控，因此式 (10) 简化为：



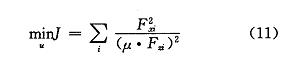
改写为矩阵形式如下：



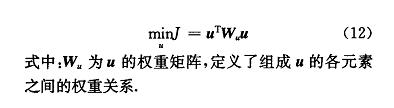
2.2.2.3 分配算法的计算

根据以上描述，在广义逆法基础上采用数学规划法中的二次规划法实现分配算法的具体计算。一般的二次规划可表述为：



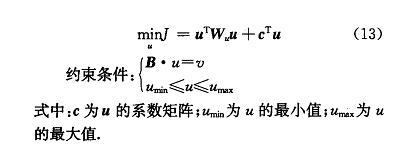
取二次部分为优化目标：



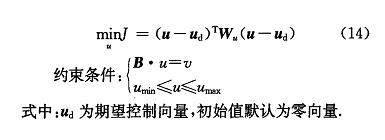
由式 (8) 可知，将等式约束 B·u = v 转化为 min lI B·u - v lI_2：，成为优化目标的一部分，则式 (14) 转化为 SLS 问题：



SLS 问题先保证满足式 (15) 的第二式，在此前提下寻求符合式 (15) 的第一式的最优解。通过引人一个权重系数 ξ，将式 (15) 的两式结合起来，从而进一步转化为 WLS 问题，减少了计算时间，式 (16) 即其表达形式。由于式 (15) 的第二式需要首先予以满足，因此 ξ 通常取得很大：



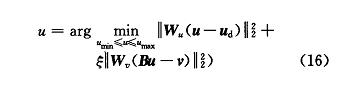
通过有效集算法求解 WLS 问题。考虑带有约束范围的最小二乘问题：



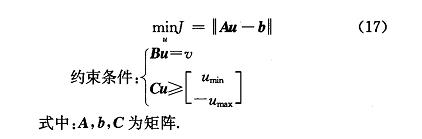
其中，车辆控制所需的广义力为：



控制变量为 4 个车轮的纵向力为：



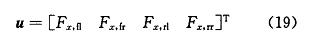
效率矩阵为：



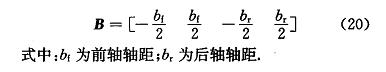
F_xi 受 μ_i，F_zi 以及 F_yi 耦合的约束如下：



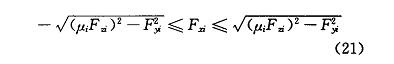
同时 μ_min 和 μ_max 上文制定的转矩分配策略有关。

在优化分配控制下，理想质心侧偏角和实际质心侧偏角的偏差并不是时刻最优的。优化分配控制策略中的约束条件不考虑质心侧偏角的偏差。各控制变量的权重矩阵 W_u 为：



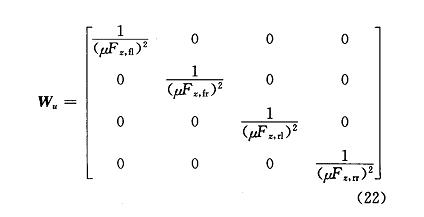
W_v 为广义力的权重矩阵，由于本文不考虑车辆施加驱动力，所研究问题中广义力仅横摆力矩一项，取 W_v 为 1 维单位矩阵。



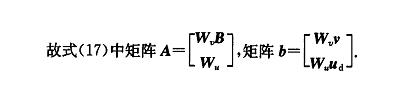
令 μ_0 为一满足式 (17) 约束条件的可行起始点，取为 4 行 1 列的零矩阵。W 是工作集，是一个 4 行 1 列的列向量。令 W 包含 μ_0 点的有效不等式约束。当 k = 0，1，2，……，N一1 时，给定 μ_k，寻找优化扰动量 p，将工作集 W 中的约束等效为等式约束，忽略剩余的不等式约束。求解：



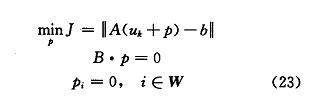
（1）如果 μ_k + p 是可行解，令 μ_(k+1) = μ_k + p 并计算拉格朗日乘子 [ μ k ]^T。拉格朗日乘子由下式决定：



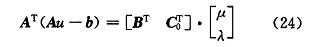
如果所有的 λ ≥ 0，则 μ_(k+1) 是优化解，结束所有计算；如果所有的 λ < 0，则去掉工作集 W 中最小的 λ 所对应的约束条件，继续进行下一个循环。

（2）如果 μ_k + p 不是可行解，则选取一个使 μ_(k+1) = μ_k + αp 是可行解的最大步长 α，在工作集 W 中添加主边界约束条件，继续进行下一个循环。


2.2.3 目标轮缸压力的计算

由此可知，计算出的附加横摆力矩根据上文提到的方法分配到各车轮上，由线控制动系统控制各车轮的制动压力来实现。对于各轮缸上的制动压力计算，不考虑驾驶员踩踏板和制动防抱死系统触发，直接根据决策出的 M_D 来计算轮缸所需液压制动力，计算方法如下：




2.3 轮缸液压力控制

由系统结构和工作原理可知，与传统制动系统的液压力控制单元有所不同的是，每个轮缸仅由一个电磁阀来控制液压力。又因为该系统是一个时变非线性系统 [2]，难以精确建模，并且系统的动态响应不能用简单的模型来表示。因此设计控制器时需要考虑其参数和阶次在不同时刻不同工作点处的适应性。为了简化控制器设计并达到 YSC 功能实现的要求，轮缸液压力控制采用主缸定频调压法。

主缸定频调压法的工作原理如下：当 4 个轮缸提出各自的目标压力时，令电机推动主缸活塞作往复抖动，从而使主缸压力不断抖动，令主缸的压力幅值范围覆盖 4 个轮缸的目标压力，且其抖动的压力频率大大高于各轮缸目标压力的频率，每当主缸压力靠近轮缸的目标压力时，适时地开闭电磁阀以使轮缸压力跟踪目标压力变化。



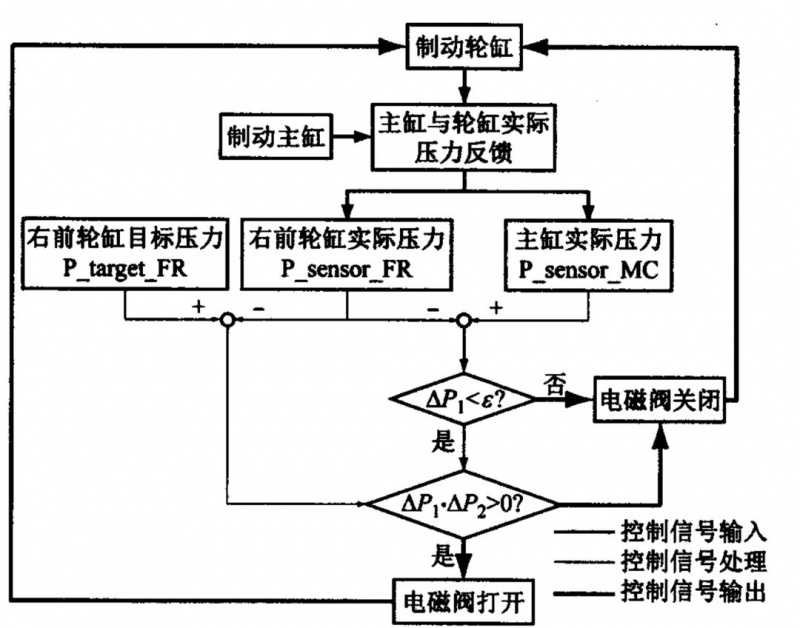
图 6 主缸定频调压法的电磁阀控制逻辑框图

如图 6 所示为主缸定频调压法的电磁阀控制逻辑框图。在判断轮缸目标压力与轮缸实际压力之差和主缸实际压力与轮缸实际压力之差符号是否相同之前，先对实际主缸压力与轮缸实际压力之差的大小进行判断，当两者压力差过大时直接关闭电磁阀给轮缸保压。这是由于给电磁阀关闭指令到电磁阀真正实现关闭需要一段时间，当主缸实际压力与轮缸实际压力相差较大时会造成轮缸压力控制发生很大的超调，降低了控制的精度。


3. 台架试验验证

为了验证提出的车辆稳定性优化控制算法的有效性，基于搭建的硬件在环试验台架分别在低附和高附路面上进行蛇行工况试验。设置低附路面附着系数为 0.2，车速为 54 km/h；高附路面附着系数为 0.8，车速为 106 km/h。



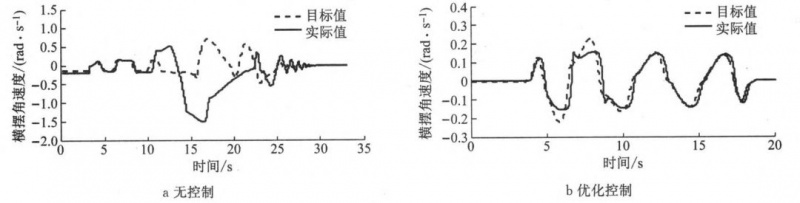
图 7 低附路面横摆角速度响应曲线

由图 7 可知，在低附路面无控制时，横摆角速度在 12～22 s 出现较大误差，在 15～20 s 之间实际值严重偏离了目标值，且实际值变化幅度较大，甚至实际值的方向与目标值的方向相反，会导致车辆失稳不可控。而低附路面优化控制时，横摆角速度跟踪误差较小，相比无控制时大大提高了车辆稳定性和安全性。



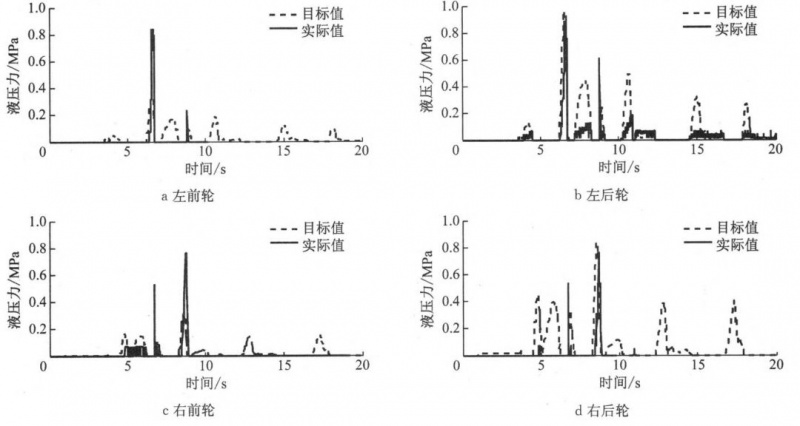
图 8 低附路面优化控制时各车轮轮缸压力响应曲线

图 8 为低附路面优化控制时各车轮轮缸压力响应。由图可知，液压力控制虽然有一定误差，但能够满足车辆稳定性控制的要求。



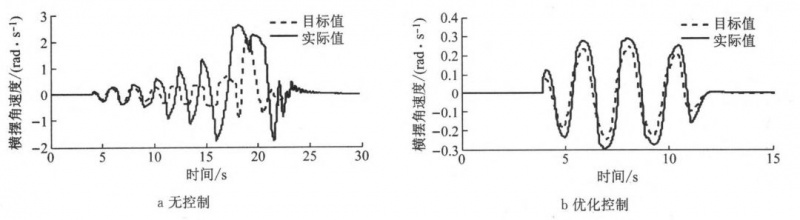
9 高附路面横摆角速度响应曲线

由图 9 可知，在高附路面无控制时，横摆角速度的误差越来越大，会导致车辆失稳不可控；而加入优化控制后，横摆角速度跟踪误差较小，相比无控制时提高了车辆稳定性和安全性。



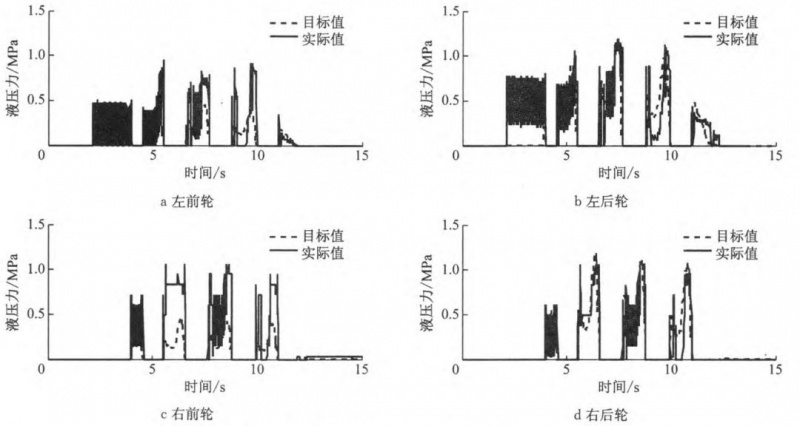
图 10 高附路面优化控制时各车轮轮缸压力响应曲线

图 10 为高附路面优化控制时各车轮轮缸压力响应。由图可知，实际液压力能够快速跟随目标液压力，超调压力较小，并且波形稳定，能够满足车辆稳定性控制的要求。从试验结果来看，不论是在低附或高附路面上，有优化控制时的 YSC 效果均比无控制时好，有效改善了车辆的稳定性，并且在高附着系数路面上液压力控制效果更好。


4. 结论

提出了基于线控制动系统的车辆稳定性优化控制策略。

首先以线性二自由度车辆模型为参考模型，求出目标横摆角速度，并与实际横摆角速度求差，利用 PI 控制算法求出附加横摆力矩。

再根据所计算出的车辆附加横摆力矩、方向盘转角来识别车辆实际行驶特性，然后通过广义逆法和数学归划法相结合的方法将附加横摆力矩分配到作用车轮上，由基于主缸定频调压法的线控制动系统进行轮缸液压力控制。

台架试验结果表明，本文提出的车辆稳定性优化控制策略能够有效地保证车辆在高低附路面工况下的稳定性和安全性。


参考文献